Prof D’s Regression Sessions - Vol 2

AKA - Multiple Regression

Preamble

We’re going even deeper this week in Volume 2 of the Regression Sessions, so to help you along on your journey we have got Volume 2 of the Progression Sessions with Blame and DRS - Enjoy!

Introduction

Similar to last week’s practical, we will continue our investigation into the factors that affect school-level attainment figures, following the lecture you have just seen.

Last week, you created a data subset for England of some 30-odd variables related to different measures of attainment, and a selection of continuous and categorical variables which might help explain those attainment levels. This week we will use more of those variables to build a multiple regression model and evaluate its outputs.

Building a good regression model can be as much art as it is science! Back to our cake baking analogy last week - think of it a bit like the bake-off ‘technical challenge’ - same recipe, same ingredients, potentially some very different outcomes!

It takes a lot of practice, iteration and understanding of the various dimensions in your model to build a good regression model. It is much more than just a good R-squared and some ‘statistically significant’ coefficients!

Aims

By the end of this week’s regression session you should:

Consolidate your knowledge of using R or Python to process data in order to carry out a scientific investigation
Build on the skills learned last week to practice further plotting and visualising of data to assess relationships between multiple x variables and a selected y variable
Refresh your knowledge of using built-in statistical software functions in R and Python to run some more sophisticated regression models and produce statistical outputs from those models
Practice interpreting the outputs of those models thinking in particular about issues of confounding, mediating, multicollinearity and the independence of residuals
Practice experimenting with interaction effects in your model and the interpretation of those outputs

Note

As with last week’s practical you will find code-blocks that will allow you to run your analysis in either R or Python. Again, it’s up to you which you decide to use.

Tasks

This week we won’t look at individual local authorities, but will focus on the whole of England.

1. Baseline Model

Run your baseline bivariate, whole of England, regression model from last week

2. Data Prep and Exploratory Data Analysis

Prepare your data and carry out some exploratory data analysis to understand what you are working with

3. Multiple Regression Model

Experiment with adding additional explanatory variables one-by-one into your model - both continuous and categorical. You might even experiment with reclassifying variables to reduce any noise that might exist with excessive categories unclear continuous relationships
Try to find the model that best explains your attainment variable. One that strikes a good balance between:
- explanatory power (a good \(R^2\), significant explanatory variables) - best doesn’t necessarily mean the highest \(R^2\), if a variable with more nuance allows you to say something more interesting about a relationship.
- parsimony (the principle of simplicity - fewest variables, simplest possible explanation)

4. Evaluation

When you have your ‘best’ model, how do you interpret the coefficients?
- Which variable(s) has(have) the most explanatory power (check t-values for this)?
- How do you interpret the combined explanatory power of variables in your model?
- What kind of confounding do you observe as you add more variables (if any)?
- Do you have any issues of multicollinearity or residual independence? Does your model pass the standard tests?

5. Interaction Effects

Experiment with interacting some of the variables in your best multiple regression model and see if this adds any more explanatory nuance to your main analysis

Task 1 - Baseline Model

First read in your data file from last week and run your final baseline model from last week
Then run a basic bivariate regression model for your attainment variable of choice (I am using raw Attainment 8 scores - ATT8SCR - , but last week you should have chosen one of the other different Attainment scores to try and model - therefore you will need to adjust your code accordingly)
Your choice of independent variable can be anything, but you might want to start with PTFSM6CLA1A (% of pupils at the end of key stage 4 who are disadvantaged) as I am.
Don’t forget, you probably will want to log-transform both of your variables

Note

The paths in the code below are specific to my home computer - you’ll need to adapt this code to read the csv from where it is on your computer.

And one more reminder - you will also need to change the variables to the ones you used last week - don’t just copy mine!

Code

import pandas as pd
import numpy as np
import janitor
from pathlib import Path
import statsmodels.api as sm

# little function to define the file root on different machines
def find_qm_root(start_path: Path = Path.cwd(), anchor: str = "QM") -> Path:
    """
    Traverse up from the start_path until the anchor folder (e.g. 'QM' or 'QM_Fork')      is found. Returns the path to the anchor folder.
    """
    for parent in [start_path] + list(start_path.parents):
        if parent.name == anchor:
            return parent
    raise FileNotFoundError(f"Anchor folder '{anchor}' not found in path      hierarchy.")
  
qm_root = find_qm_root()
base_path = qm_root / "sessions" / "L6_data" / "Performancetables_130242" / "2022-2023"
na_all = ["", "NA", "SUPP", "NP", "NE", "SP", "SN", "LOWCOV", "NEW", "SUPPMAT", "NaN"]

england_filtered = pd.read_csv(base_path / "england_filtered.csv", na_values=na_all, dtype={"URN": str})

# Log-transform safely: replace non-positive values with NaN
england_filtered['log_ATT8SCR'] = np.where(england_filtered['ATT8SCR'] > 0, np.log(england_filtered['ATT8SCR']), np.nan)
england_filtered['log_PTFSM6CLA1A'] = np.where(england_filtered['PTFSM6CLA1A'] > 0, np.log(england_filtered['PTFSM6CLA1A']), np.nan)

# Drop rows with NaNs in either column
england_filtered_clean = england_filtered.dropna(subset=['log_ATT8SCR', 'log_PTFSM6CLA1A'])

# Define independent and dependent variables
X = sm.add_constant(england_filtered_clean['log_PTFSM6CLA1A'])  # adds intercept
y = england_filtered_clean['log_ATT8SCR']

# Fit the model
england_model1 = sm.OLS(y, X).fit()
#england_summary = extract_model_summary(england_model1, 'England Model')

# Print summary
print(england_model1.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:            log_ATT8SCR   R-squared:                       0.468
Model:                            OLS   Adj. R-squared:                  0.468
Method:                 Least Squares   F-statistic:                     2611.
Date:                Tue, 09 Dec 2025   Prob (F-statistic):               0.00
Time:                        21:03:32   Log-Likelihood:                 1668.0
No. Observations:                2968   AIC:                            -3332.
Df Residuals:                    2966   BIC:                            -3320.
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
===================================================================================
                      coef    std err          t      P>|t|      [0.025      0.975]
-----------------------------------------------------------------------------------
const               4.4778      0.013    349.542      0.000       4.453       4.503
log_PTFSM6CLA1A    -0.2071      0.004    -51.095      0.000      -0.215      -0.199
==============================================================================
Omnibus:                      105.763   Durbin-Watson:                   1.313
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              199.209
Skew:                           0.267   Prob(JB):                     5.53e-44
Kurtosis:                       4.151   Cond. No.                         17.5
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Code

library(tidyverse)
library(janitor)
library(readr)
library(dplyr)
library(here)

base_path <- here("sessions", "L6_data", "Performancetables_130242", "2022-2023")
na_all <- c("", "NA", "SUPP", "NP", "NE", "SP", "SN", "LOWCOV", "NEW", "SUPPMAT")

england_filtered <- read_csv(file.path(base_path, "england_filtered.csv"), na = na_all) |> mutate(URN = as.character(URN))

#str(england_filtered)

england_filtered_clean <- england_filtered[
  !is.na(england_filtered$ATT8SCR) & 
  !is.na(england_filtered$PTFSM6CLA1A) &
  england_filtered$ATT8SCR > 0 &
  england_filtered$PTFSM6CLA1A > 0, 
]

# Fit linear model and get predicted values
england_model1 <- lm(log(ATT8SCR) ~ log(PTFSM6CLA1A), data = england_filtered_clean)
summary(england_model1)


Call:
lm(formula = log(ATT8SCR) ~ log(PTFSM6CLA1A), data = england_filtered_clean)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.65843 -0.08607 -0.00897  0.07800  0.55670 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)       4.477823   0.012811  349.54   <2e-16 ***
log(PTFSM6CLA1A) -0.207090   0.004053  -51.09   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.138 on 2966 degrees of freedom
Multiple R-squared:  0.4681,    Adjusted R-squared:  0.468 
F-statistic:  2611 on 1 and 2966 DF,  p-value: < 2.2e-16

Task 2 - Exploratory Analysis and Data Preparation

Right, we that was a nice and simple starter. We now have a baseline and something to compare your subsequent more sophisticated models to.
These next steps will be a little trickier and I will be expecting you to use some of the knowledge gained last week to complete the tasks, rather than me giving you all of the right code explicitly.

Code

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Drop unwanted numeric columns
numeric_cols = england_filtered_clean.drop(columns=['easting', 'northing', 'LEA'], errors='ignore').select_dtypes(include='number')

# Convert to long format
numeric_long = numeric_cols.melt(var_name='variable', value_name='value')

# Set up the figure
variables = numeric_long['variable'].unique()
n_vars = len(variables)
cols = 6
rows = (n_vars + cols - 1) // cols

fig, axes = plt.subplots(rows, cols, figsize=(18, 3 * rows))
axes = axes.flatten()

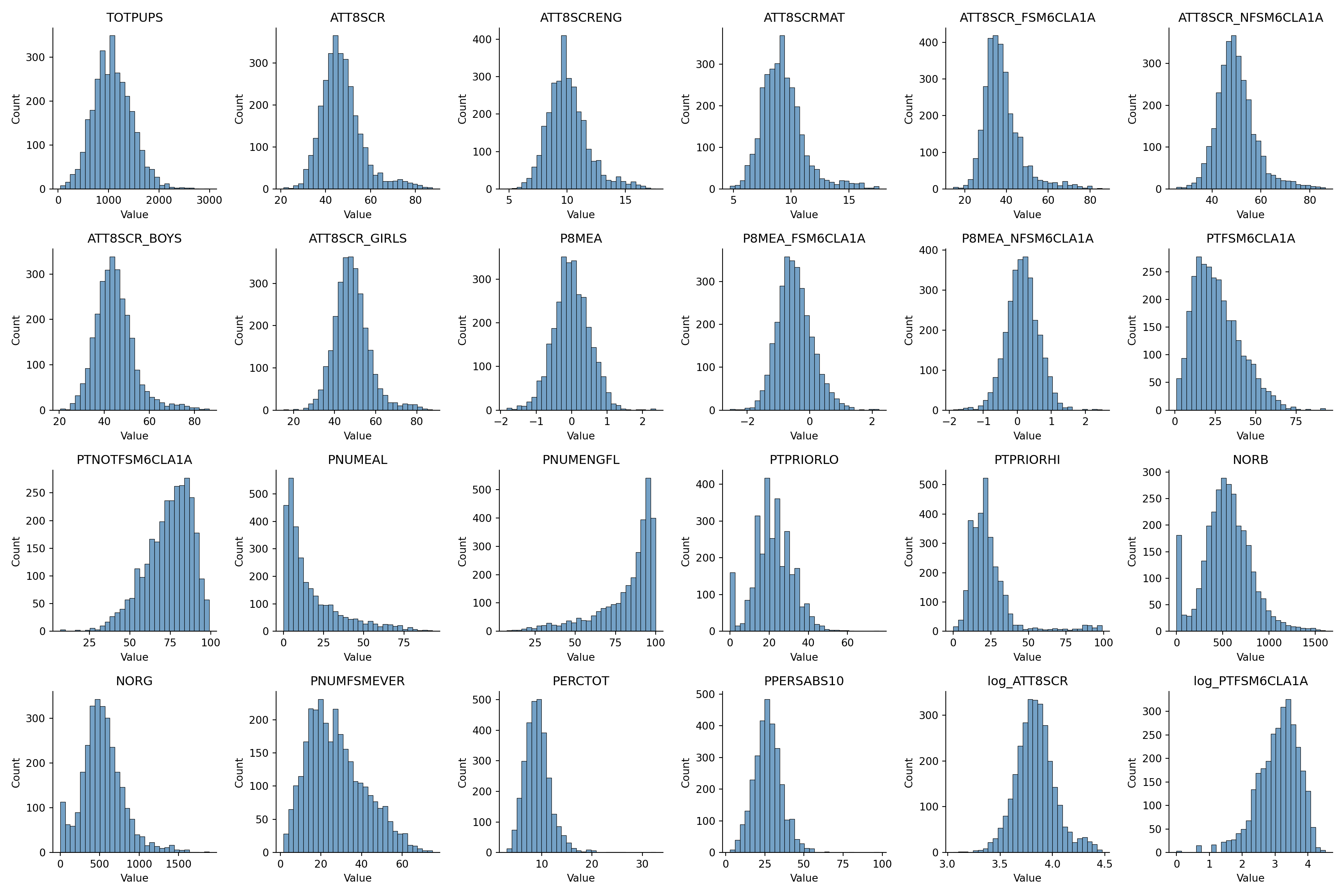
for i, var in enumerate(variables):
    sns.histplot(data=numeric_long[numeric_long['variable'] == var], x='value', bins=30, color='steelblue', ax=axes[i])
    axes[i].set_title(var)
    axes[i].set_xlabel("Value")
    axes[i].set_ylabel("Count")

# Hide unused subplots
for j in range(i + 1, len(axes)):
    fig.delaxes(axes[j])

plt.tight_layout()
plt.suptitle("Histograms of Numerical Variables", y=1.02)
sns.despine()
plt.show()

Code

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np

# Log-transform relevant variables
england_filtered_clean['log_ATT8SCR'] = np.log(england_filtered_clean['ATT8SCR'])
england_filtered_clean['log_PTFSM6CLA1A'] = np.log(england_filtered_clean['PTFSM6CLA1A'])
england_filtered_clean['log_PNUMEAL'] = np.log(england_filtered_clean['PNUMEAL'])
england_filtered_clean['log_PERCTOT'] = np.log(england_filtered_clean['PERCTOT'])

# Prepare long format data
long_df = pd.melt(
    england_filtered_clean,
    id_vars=['log_ATT8SCR'],
    value_vars=['log_PTFSM6CLA1A', 'log_PNUMEAL', 'log_PERCTOT', 'PTPRIORLO'],
    var_name='predictor',
    value_name='x_value'
)

# Custom axis labels
axis_labels = {
    'log_PTFSM6CLA1A': 'log(PTFSM6CLA1A)',
    'log_PNUMEAL': 'log(PNUMEAL)',
    'log_PERCTOT': 'log(PERCTOT)',
    'PTPRIORLO': 'PTPRIORLO'
}

# Set up the figure manually
predictors = long_df['predictor'].unique()
cols = 2
rows = (len(predictors) + cols - 1) // cols
fig, axes = plt.subplots(rows, cols, figsize=(12, 4 * rows))
axes = axes.flatten()

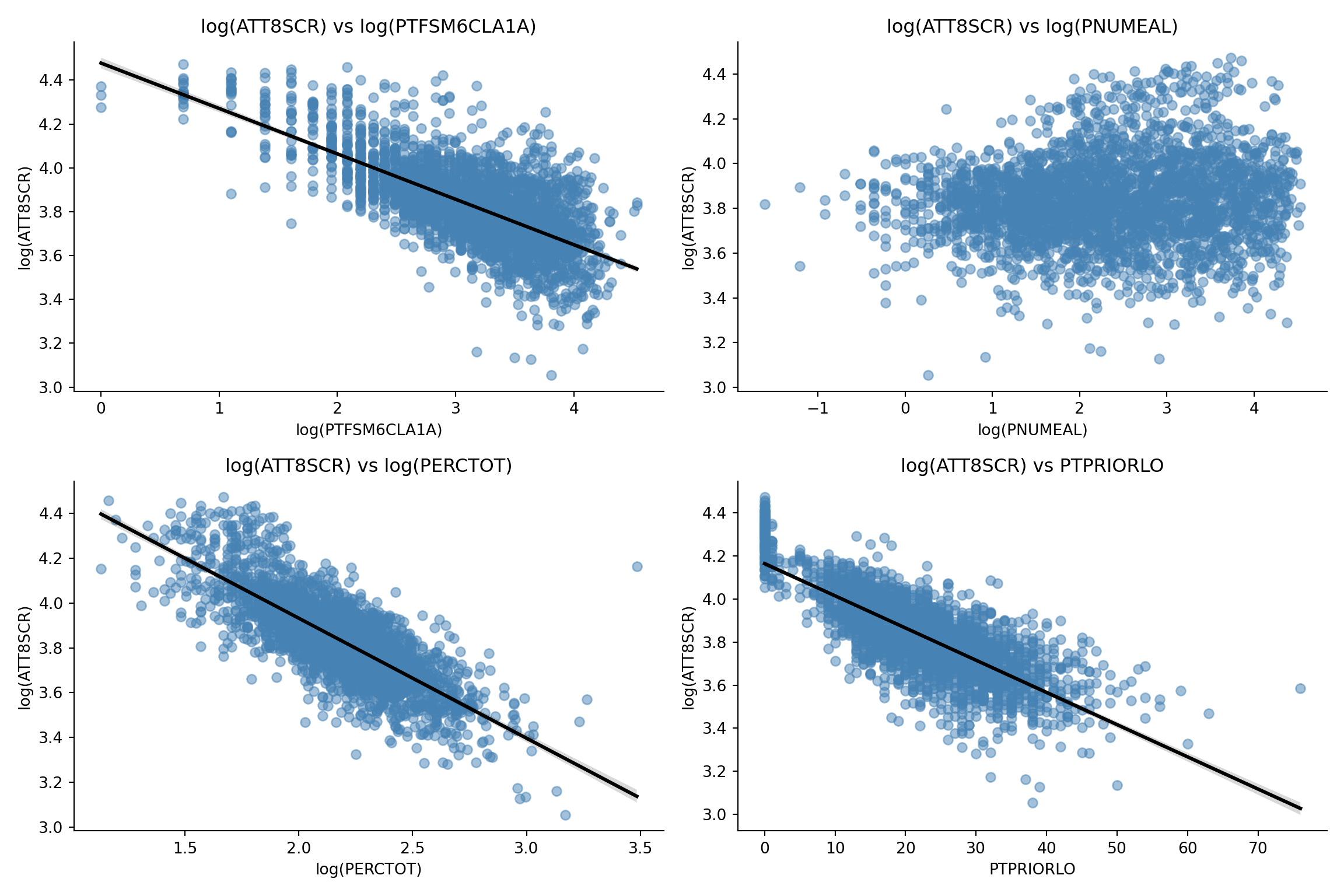
for i, predictor in enumerate(predictors):
    subset = long_df[long_df['predictor'] == predictor]
    sns.regplot(
        data=subset,
        x='x_value',
        y='log_ATT8SCR',
        scatter_kws={'alpha': 0.5, 'color': 'steelblue'},
        line_kws={'color': 'black'},
        ax=axes[i]
    )
    axes[i].set_title(f"log(ATT8SCR) vs {axis_labels[predictor]}")
    axes[i].set_xlabel(axis_labels[predictor])
    axes[i].set_ylabel("log(ATT8SCR)")

# Hide unused subplots
for j in range(i + 1, len(axes)):
    fig.delaxes(axes[j])

plt.tight_layout()
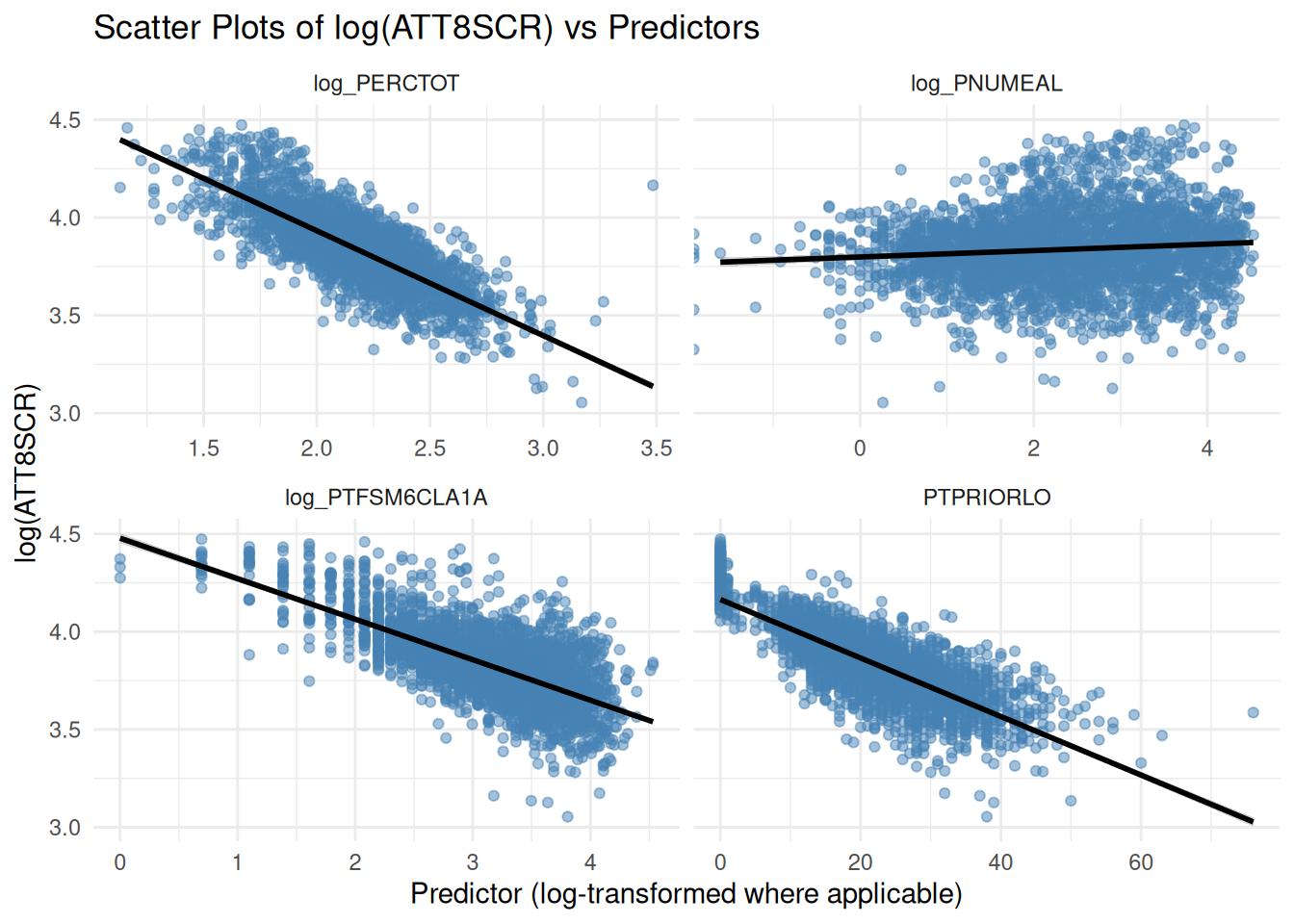
plt.suptitle("Scatter Plots of log(ATT8SCR) vs Predictors", y=1.02)
sns.despine()
plt.show()

Code

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Select categorical columns and drop unwanted ones
categorical_cols = england_filtered_clean.select_dtypes(include='object').drop(
    columns=['URN', 'SCHNAME.x', 'LANAME', 'TOWN.x', 'SCHOOLTYPE.x'], errors='ignore'
)

# Determine layout
n_cols = 2
n_rows = (len(categorical_cols.columns) + n_cols - 1) // n_cols
fig, axes = plt.subplots(n_rows, n_cols, figsize=(12, 4 * n_rows))
axes = axes.flatten()

# Generate bar plots
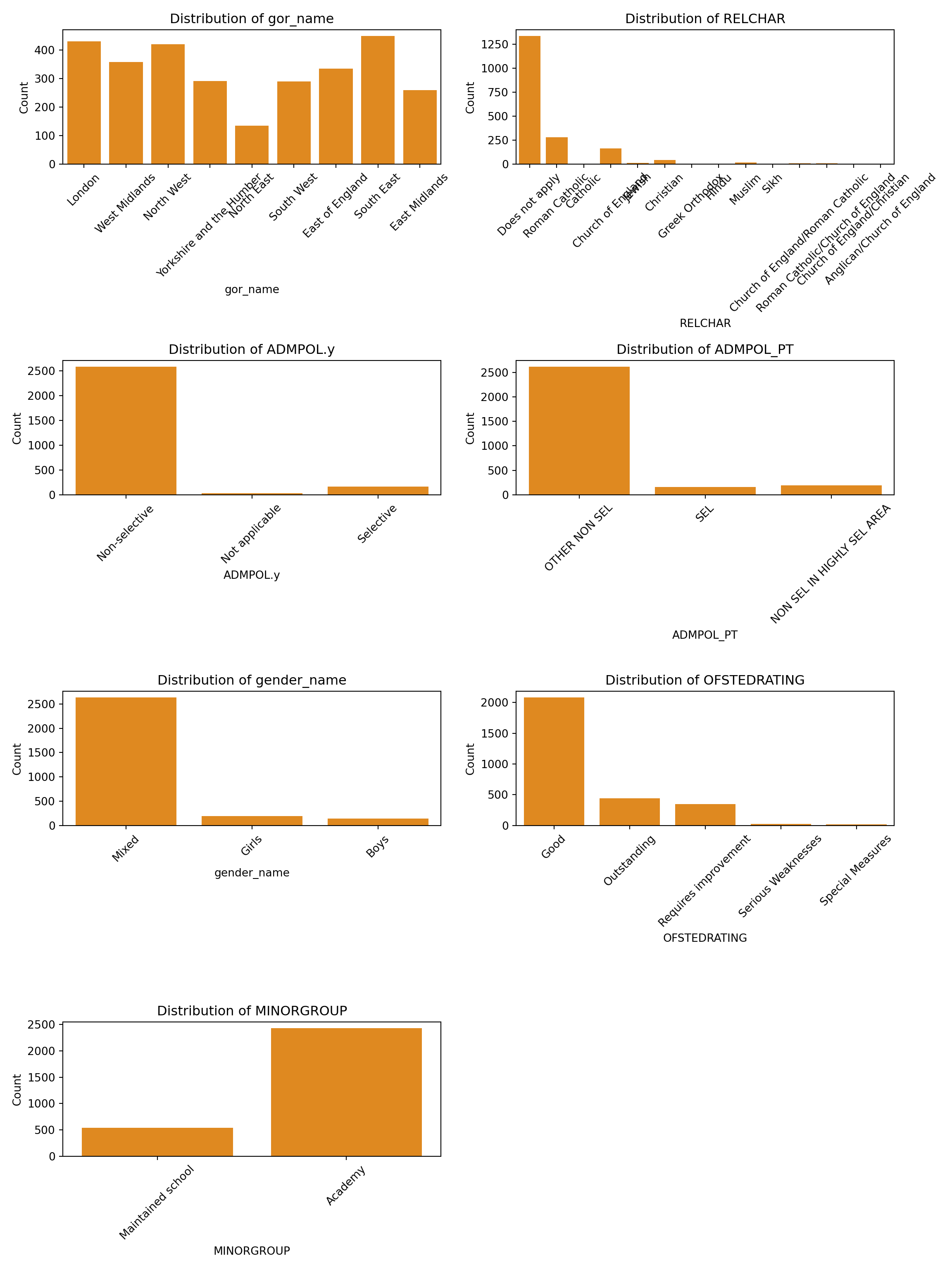
for i, colname in enumerate(categorical_cols.columns):
    sns.countplot(data=categorical_cols, x=colname, ax=axes[i], color='darkorange')
    axes[i].set_title(f"Distribution of {colname}")
    axes[i].set_xlabel(colname)
    axes[i].set_ylabel("Count")
    axes[i].tick_params(axis='x', rotation=45)

# Hide unused subplots
for j in range(i + 1, len(axes)):
    fig.delaxes(axes[j])

plt.tight_layout()
plt.show()

Code

library(tidyverse)

# Select only numeric columns
numeric_cols <- england_filtered_clean %>% 
  select(where(is.numeric)) %>% 
  select(-easting, -northing, -LEA)

# Convert to long format for faceting
numeric_long <- numeric_cols %>%
  pivot_longer(cols = everything(), names_to = "variable", values_to = "value")

# Plot faceted histograms
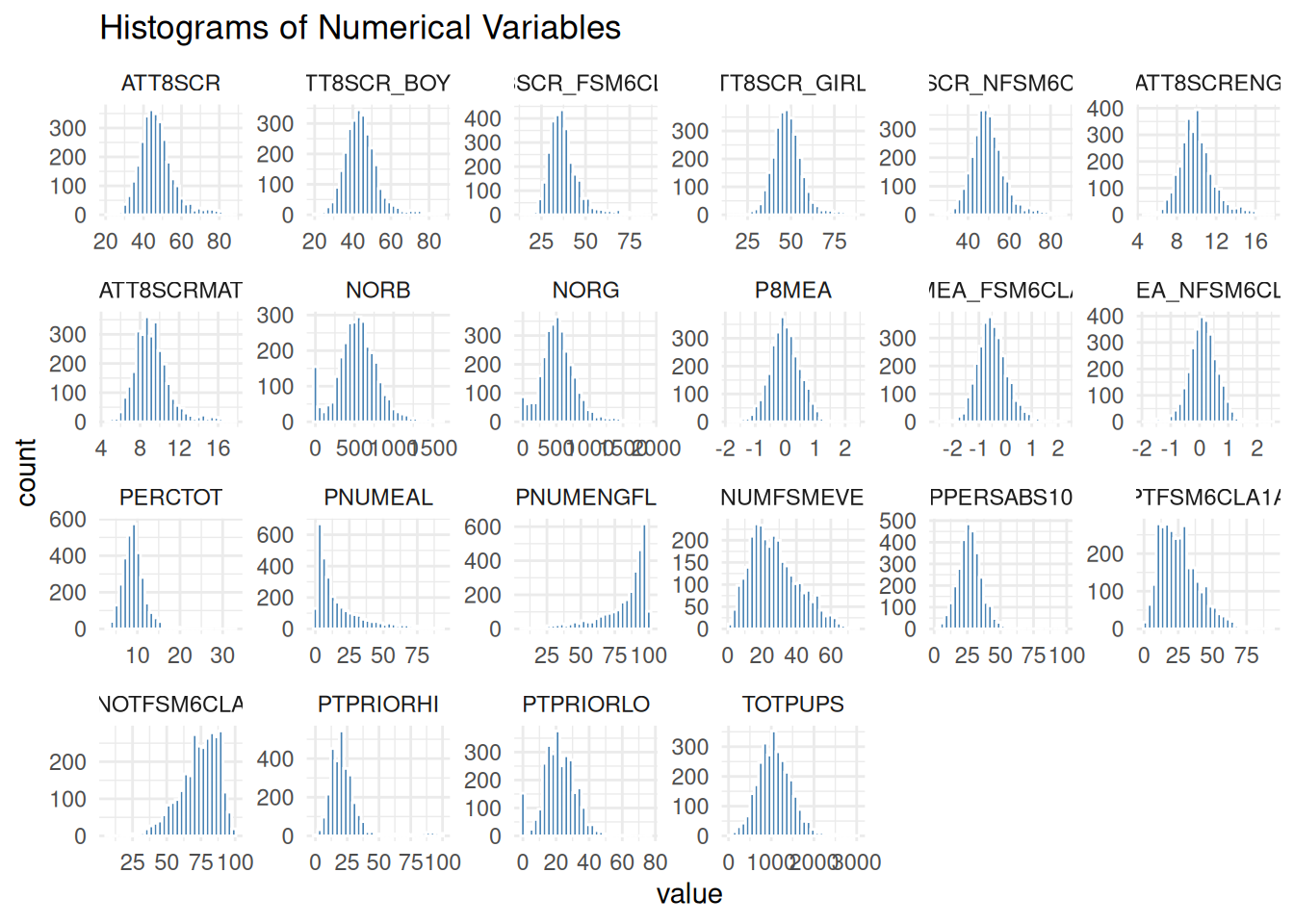
ggplot(numeric_long, aes(x = value)) +
  geom_histogram(bins = 30, fill = "steelblue", color = "white") +
  facet_wrap(~ variable, scales = "free", ncol = 6) +
  theme_minimal() +
  labs(title = "Histograms of Numerical Variables")

Code

library(tidyverse)

# Prepare the data
scatter_data <- england_filtered_clean %>%
  select(ATT8SCR, PTFSM6CLA1A, PNUMEAL, PERCTOT, PTPRIORLO) %>%
  mutate(
    log_ATT8SCR = log(ATT8SCR),
    log_PTFSM6CLA1A = log(PTFSM6CLA1A),
    log_PNUMEAL = log(PNUMEAL),
    log_PERCTOT = log(PERCTOT)
  ) %>%
  pivot_longer(
    cols = c(log_PTFSM6CLA1A, log_PNUMEAL, log_PERCTOT, PTPRIORLO),
    names_to = "predictor",
    values_to = "x_value"
  )

# Create faceted scatter plots
ggplot(scatter_data, aes(x = x_value, y = log_ATT8SCR)) +
  geom_point(alpha = 0.5, color = "steelblue") +
  geom_smooth(method = "lm", se = TRUE, color = "black") +
  facet_wrap(~ predictor, scales = "free_x") +
  theme_minimal() +
  labs(
    title = "Scatter Plots of log(ATT8SCR) vs Predictors",
    x = "Predictor (log-transformed where applicable)",
    y = "log(ATT8SCR)"
  )

Code

library(tidyverse)
library(cowplot)

# Drop unwanted columns
categorical_cols <- england_filtered_clean %>%
  select(where(is.character)) %>%
  select(-URN, -SCHNAME.x, -LANAME, -TOWN.x, -SCHOOLTYPE.x)

# Create a list to store plots (unnamed)
plot_list <- list()

# Loop through each categorical column and generate a bar plot
for (colname in names(categorical_cols)) {
  p <- ggplot(categorical_cols, aes_string(x = colname)) +
    geom_bar(fill = "darkorange") +
    theme_minimal() +
    labs(title = paste("Distribution of", colname), x = colname, y = "Count") +
    theme(axis.text.x = element_text(angle = 45, hjust = 1))
  
  plot_list <- append(plot_list, list(p))  # Append without naming
}

# Combine all plots into a single figure
combined_plot <- cowplot::plot_grid(plotlist = plot_list, ncol = 2)
print(combined_plot)

Changing your dummy reference category

Your dummy variable reference category is the category within the variable that all other categories will be compared against in your model.

While the reference category has no effect on the model itself, it does make a difference for how you interpret your model.

For example, if you are using Regions in England as a dummy, setting your reference region as London will mean all other regions are compared to it and they might naturally be lower or higher.

A good strategy is to select the most or least numerous or important category in your variable, rather than something in the middle. Of course, you may not know which is most important until you run your model, so you may need to go back and reset the reference variable and run the model again.

Here is some code in R and Python to help you carry out the setting of the reference level (Yes, it’s more straightforward in R!)

Code

import pandas as pd
from pandas.api.types import CategoricalDtype

# Ensure it's a copy to avoid SettingWithCopyWarning
england_filtered_clean = england_filtered_clean.copy()

# Set reference level for gor_name
gor_dtype = CategoricalDtype(
    categories=["South East"] + sorted(set(england_filtered_clean["gor_name"]) - {"South East"}),
    ordered=True
)
england_filtered_clean["gor_name"] = england_filtered_clean["gor_name"].astype(gor_dtype)

# Set reference level for ofsted_rating_name
ofsted_dtype = CategoricalDtype(
    categories=["Good"] + sorted(set(england_filtered_clean["OFSTEDRATING"].dropna()) - {"Good"}),
    ordered=True
)
england_filtered_clean["ofsted_rating_name"] = england_filtered_clean["OFSTEDRATING"].astype(ofsted_dtype)

# Set reference level for ADMPOL_PT
admpol_dtype = CategoricalDtype(
    categories=["OTHER NON SEL"] + sorted(set(england_filtered_clean["ADMPOL_PT"]) - {"OTHER NON SEL"}),
    ordered=True
)
england_filtered_clean["ADMPOL_PT"] = england_filtered_clean["ADMPOL_PT"].astype(admpol_dtype)

Code

## In R, you can change the reference category using the relevel() function

england_filtered_clean$gor_name <- relevel(factor(england_filtered_clean$gor_name), ref = "South East")
england_filtered_clean$ofsted_rating_name <- relevel(factor(england_filtered_clean$OFSTEDRATING), ref = "Good")
england_filtered_clean$ADMPOL_PT <- relevel(factor(england_filtered_clean$ADMPOL_PT), ref = "OTHER NON SEL")

Reclassifying a variable into fewer categories

As mentioned in the lecture, it can sometimes be useful to reclassify a variable into fewer categories to see if a signal appears.

Let’s have a look at the religious character of a school variable and test it out as dummy in a basic model:

Note the Python code is far more complicated than the R code, but should prodice similar outputs

Code

import numpy as np
import pandas as pd
import statsmodels.api as sm

# Drop rows with missing values in relevant columns
model_df = england_filtered_clean[['ATT8SCR', 'PTFSM6CLA1A', 'RELCHAR']].dropna().copy()

# Log-transform numeric variables
model_df['log_ATT8SCR'] = np.log(model_df['ATT8SCR'].astype(float))
model_df['log_PTFSM6CLA1A'] = np.log(model_df['PTFSM6CLA1A'].astype(float))

# Ensure RELCHAR is treated as categorical
model_df['RELCHAR'] = model_df['RELCHAR'].astype('category')

# Create design matrix with dummy variables for RELCHAR
X = pd.get_dummies(model_df[['log_PTFSM6CLA1A', 'RELCHAR']], drop_first=True)

# Add constant
X = sm.add_constant(X)

# Response variable
y = model_df['log_ATT8SCR']

# Ensure all columns are float64 to avoid dtype issues
X = X.astype('float64')
y = y.astype('float64')

# Fit linear model using Pandas DataFrame directly
model = sm.OLS(y, X).fit()

# Display summary with proper variable names
print(model.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:            log_ATT8SCR   R-squared:                       0.429
Model:                            OLS   Adj. R-squared:                  0.424
Method:                 Least Squares   F-statistic:                     99.29
Date:                Tue, 09 Dec 2025   Prob (F-statistic):          3.44e-213
Time:                        21:03:47   Log-Likelihood:                 1138.8
No. Observations:                1868   AIC:                            -2248.
Df Residuals:                    1853   BIC:                            -2165.
Df Model:                          14                                         
Covariance Type:            nonrobust                                         
============================================================================================================
                                               coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------------------------------------
const                                        4.2730      0.134     31.939      0.000       4.011       4.535
log_PTFSM6CLA1A                             -0.1860      0.005    -34.224      0.000      -0.197      -0.175
RELCHAR_Catholic                             0.1769      0.153      1.159      0.246      -0.122       0.476
RELCHAR_Christian                            0.2358      0.134      1.763      0.078      -0.027       0.498
RELCHAR_Church of England                    0.1498      0.133      1.130      0.259      -0.110       0.410
RELCHAR_Church of England/Christian          0.1546      0.187      0.827      0.408      -0.212       0.521
RELCHAR_Church of England/Roman Catholic     0.0989      0.141      0.700      0.484      -0.178       0.376
RELCHAR_Does not apply                       0.1255      0.132      0.950      0.342      -0.134       0.385
RELCHAR_Greek Orthodox                       0.1586      0.187      0.849      0.396      -0.208       0.525
RELCHAR_Hindu                                0.2145      0.187      1.146      0.252      -0.152       0.581
RELCHAR_Jewish                               0.1289      0.138      0.935      0.350      -0.141       0.399
RELCHAR_Muslim                               0.4221      0.136      3.106      0.002       0.156       0.689
RELCHAR_Roman Catholic                       0.1755      0.132      1.325      0.185      -0.084       0.435
RELCHAR_Roman Catholic/Church of England     0.0789      0.145      0.546      0.585      -0.205       0.363
RELCHAR_Sikh                                 0.1980      0.162      1.223      0.221      -0.119       0.515
==============================================================================
Omnibus:                       54.961   Durbin-Watson:                   1.338
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              135.365
Skew:                           0.041   Prob(JB):                     4.04e-30
Kurtosis:                       4.316   Cond. No.                         561.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Code

# Fit linear model and get predicted values
england_model2 <- lm(log(ATT8SCR) ~ log(PTFSM6CLA1A) + RELCHAR, data = england_filtered_clean)
summary(england_model2)


Call:
lm(formula = log(ATT8SCR) ~ log(PTFSM6CLA1A) + RELCHAR, data = england_filtered_clean)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.64638 -0.08524 -0.00935  0.07833  0.55537 

Coefficients:
                                         Estimate Std. Error t value Pr(>|t|)
(Intercept)                              4.353703   0.136250  31.954  < 2e-16
log(PTFSM6CLA1A)                        -0.206428   0.004055 -50.910  < 2e-16
RELCHARCatholic                          0.157465   0.156284   1.008  0.31375
RELCHARChristian                         0.218783   0.136987   1.597  0.11035
RELCHARChurch of England                 0.131462   0.135766   0.968  0.33298
RELCHARChurch of England/Christian       0.122838   0.191454   0.642  0.52118
RELCHARChurch of England/Roman Catholic  0.080702   0.144692   0.558  0.57706
RELCHARDoes not apply                    0.109962   0.135391   0.812  0.41675
RELCHARGreek Orthodox                    0.133210   0.191417   0.696  0.48654
RELCHARHindu                             0.173507   0.191523   0.906  0.36504
RELCHARJewish                            0.089840   0.141044   0.637  0.52420
RELCHARMuslim                            0.410154   0.139248   2.945  0.00325
RELCHARNone                              0.120208   0.135422   0.888  0.37480
RELCHARRoman Catholic                    0.156817   0.135599   1.156  0.24758
RELCHARRoman Catholic/Church of England  0.065413   0.148244   0.441  0.65906
RELCHARSikh                              0.177106   0.165766   1.068  0.28542
                                           
(Intercept)                             ***
log(PTFSM6CLA1A)                        ***
RELCHARCatholic                            
RELCHARChristian                           
RELCHARChurch of England                   
RELCHARChurch of England/Christian         
RELCHARChurch of England/Roman Catholic    
RELCHARDoes not apply                      
RELCHARGreek Orthodox                      
RELCHARHindu                               
RELCHARJewish                              
RELCHARMuslim                           ** 
RELCHARNone                                
RELCHARRoman Catholic                      
RELCHARRoman Catholic/Church of England    
RELCHARSikh                                
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1353 on 2935 degrees of freedom
  (17 observations deleted due to missingness)
Multiple R-squared:  0.4904,    Adjusted R-squared:  0.4878 
F-statistic: 188.3 on 15 and 2935 DF,  p-value: < 2.2e-16

You will notice that the religious character variables nearly all insignificant. As such, lets try collapsing into three groups - “None”, “Christian” and “Non-Christian”

Code

# Define mapping function
def classify_relchar(value):
    if pd.isna(value):
        return "None"
    elif value in ["Does not apply", "None"]:
        return "None"
    elif value in [
        "Roman Catholic", "Greek Orthodox", "Church of England", "Catholic", "Christian",
        "Church of England/Roman Catholic", "Roman Catholic/Church of England",
        "Church of England/Christian", "Anglican/Church of England"
    ]:
        return "Christian"
    else:
        return "Non-Christian"

# Apply classification
england_filtered_clean['RELCHAR_Grp'] = england_filtered_clean['RELCHAR'].apply(classify_relchar)

Code

england_filtered_clean <- england_filtered_clean %>%
  mutate(RELCHAR_Grp = case_when(
    RELCHAR %in% c("Does not apply", "None") ~ "None",
    RELCHAR %in% c(
      "Roman Catholic", "Greek Orthodox", "Church of England", "Catholic", "Christian",
      "Church of England/Roman Catholic", "Roman Catholic/Church of England",
      "Church of England/Christian", "Anglican/Church of England"
    ) ~ "Christian",
    TRUE ~ "Non-Christian"
  ))

Now re-run your model

Code

import numpy as np
import pandas as pd
import statsmodels.api as sm

# Convert RELCHAR_Grp to a categorical variable with "None" as the reference level
england_filtered_clean['RELCHAR_Grp'] = pd.Categorical(
    england_filtered_clean['RELCHAR_Grp'],
    categories=["None", "Christian", "Non-Christian"],
    ordered=False
)

# Drop rows with missing values in relevant columns
model_df = england_filtered_clean[['ATT8SCR', 'PTFSM6CLA1A', 'RELCHAR_Grp']].dropna().copy()

# Log-transform numeric variables
model_df['log_ATT8SCR'] = np.log(model_df['ATT8SCR'].astype(float))
model_df['log_PTFSM6CLA1A'] = np.log(model_df['PTFSM6CLA1A'].astype(float))

# Ensure RELCHAR is treated as categorical
model_df['RELCHAR_Grp'] = model_df['RELCHAR_Grp'].astype('category')

# Create design matrix with dummy variables for RELCHAR
X = pd.get_dummies(model_df[['log_PTFSM6CLA1A', 'RELCHAR_Grp']], drop_first=True)

# Add constant
X = sm.add_constant(X)

# Response variable
y = model_df['log_ATT8SCR']

# Ensure all columns are float64 to avoid dtype issues
X = X.astype('float64')
y = y.astype('float64')

# Fit linear model using Pandas DataFrame directly
model = sm.OLS(y, X).fit()

# Display summary with proper variable names
print(model.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:            log_ATT8SCR   R-squared:                       0.480
Model:                            OLS   Adj. R-squared:                  0.479
Method:                 Least Squares   F-statistic:                     912.1
Date:                Tue, 09 Dec 2025   Prob (F-statistic):               0.00
Time:                        21:03:47   Log-Likelihood:                 1701.5
No. Observations:                2968   AIC:                            -3395.
Df Residuals:                    2964   BIC:                            -3371.
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
=============================================================================================
                                coef    std err          t      P>|t|      [0.025      0.975]
---------------------------------------------------------------------------------------------
const                         4.4636      0.013    348.686      0.000       4.438       4.489
log_PTFSM6CLA1A              -0.2051      0.004    -51.053      0.000      -0.213      -0.197
RELCHAR_Grp_Christian         0.0371      0.007      5.539      0.000       0.024       0.050
RELCHAR_Grp_Non-Christian     0.1544      0.024      6.347      0.000       0.107       0.202
==============================================================================
Omnibus:                       91.156   Durbin-Watson:                   1.356
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              175.557
Skew:                           0.219   Prob(JB):                     7.55e-39
Kurtosis:                       4.108   Cond. No.                         32.2
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Code

# Fit linear model and get predicted values
# Ensure RELCHAR_Grp is a factor with "None" as the reference level
england_filtered_clean <- england_filtered_clean %>%
  mutate(RELCHAR_Grp = factor(RELCHAR_Grp, levels = c("None", "Christian", "Non-Christian")))

england_model2 <- lm(log(ATT8SCR) ~ log(PTFSM6CLA1A) + RELCHAR_Grp, data = england_filtered_clean)
summary(england_model2)


Call:
lm(formula = log(ATT8SCR) ~ log(PTFSM6CLA1A) + RELCHAR_Grp, data = england_filtered_clean)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.65098 -0.08639 -0.00989  0.07850  0.56101 

Coefficients:
                          Estimate Std. Error t value Pr(>|t|)    
(Intercept)               4.467675   0.012825 348.354  < 2e-16 ***
log(PTFSM6CLA1A)         -0.206242   0.004027 -51.213  < 2e-16 ***
RELCHAR_GrpChristian      0.036648   0.006730   5.445 5.59e-08 ***
RELCHAR_GrpNon-Christian  0.080653   0.019773   4.079 4.64e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.137 on 2964 degrees of freedom
Multiple R-squared:  0.4759,    Adjusted R-squared:  0.4754 
F-statistic: 897.1 on 3 and 2964 DF,  p-value: < 2.2e-16

Has this made a difference? What’s happened to the significance of the religious character variable?

Tip

You can use this method to reclassify any different variable.

Think about how you might reclassify a continuous variable. You might think about converting something like ‘total number of pupils on roll’ into ‘small’, ‘medium’ and ‘large’ schools, for example, based on certain thresholds. How might you choose these thresholds? If you are struggling to think of how you might code this kind of reclassification up, this is exactly where AI can be very helpful in assisting you - although while it might be good at the code to do it, I can guarantee it will likely be pretty bad at deciding on useful breaks in your data, so this is where you might need to intervene.

Task 3 - Building your optimum multiple regression model

Recipe Steps

Using the steps you learned last week and the information from this week’s lecture, I would like you to find the best possible 7-dependent variable model for your chosen attainment variable (without interaction terms). These can be continuous or categorical variables or any combination of them. Remember:
- Use exploratory analysis to check the distributions of your variables using histograms, box plots etc. or binary scatter plots with your dependent variable, before putting them into your model (you’ve already done some of this, but you may need to do some more)
- you might run into issues with logging some variables that have real 0s in them - this might cause your model to break. You might need to filter these variables out of your dataset before running your model. Some of the code above will help with this - if you get stuck, ask a friendly AI for help
- with your dummy variables, you might want to experiment with changing your reference category
- you might also want to reclassify a variable if you suspect it is important, but that in its present form is coming out as insignificant
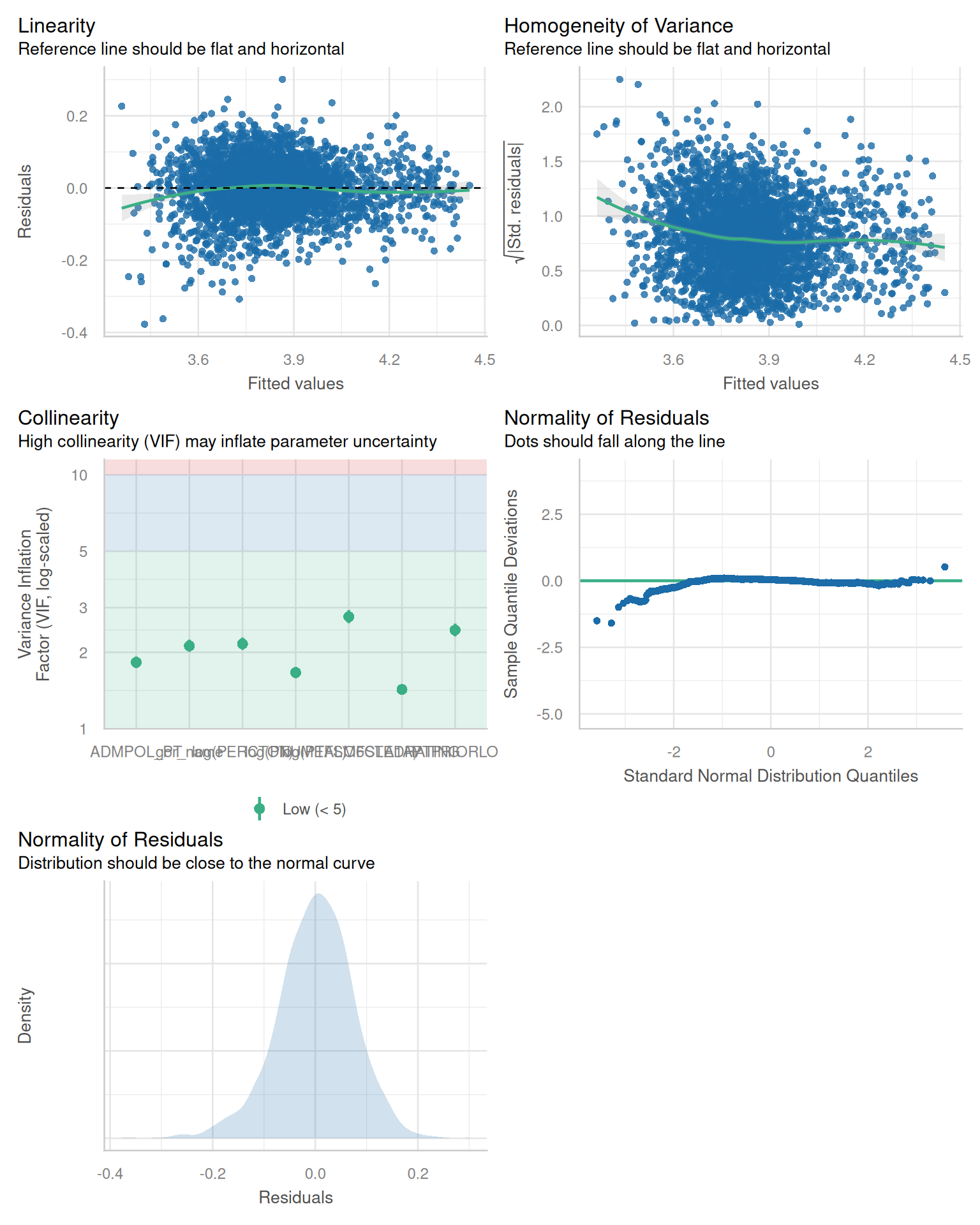
- check you regression assumptions - linearity, homoscedasticity, normality of residuals, multicollinearity, independence of residuals - does your model pass?
- which are the most important variables in your model in terms of t-values?
You should try and build your model step by step, a variable at a time. Each time you run the model, check what is happening to the coefficients
- What do you notice about confounding or mediation as you go?
- Do any of your variables become insignificant? For example, what happens to religious character groups in the presence of regions, for example? If a variable becomes insignificant, you might we wise to drop it from the analysis (but maybe not until the end in case another variable makes it significant again)

ON YOUR MARKS, GET SET - GO!!!

When you think you have your best model, move on to Task 4 below

Code

import numpy as np
import statsmodels.formula.api as smf

# Filter rows where all log-transformed variables are > 0
england_filtered_clean = england_filtered_clean[
    (england_filtered_clean['PTFSM6CLA1A'] > 0) &
    (england_filtered_clean['PERCTOT'] > 0) &
    (england_filtered_clean['PNUMEAL'] > 0)
].copy()

# Create log-transformed columns
england_filtered_clean['log_ATT8SCR'] = np.log(england_filtered_clean['ATT8SCR'])
england_filtered_clean['log_PTFSM6CLA1A'] = np.log(england_filtered_clean['PTFSM6CLA1A'])
england_filtered_clean['log_PERCTOT'] = np.log(england_filtered_clean['PERCTOT'])
england_filtered_clean['log_PNUMEAL'] = np.log(england_filtered_clean['PNUMEAL'])

# Fit the model
model = smf.ols(
    formula='log_ATT8SCR ~ log_PTFSM6CLA1A + log_PERCTOT + log_PNUMEAL + OFSTEDRATING + gor_name + PTPRIORLO + ADMPOL_PT',
    data=england_filtered_clean
).fit()

print(model.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:            log_ATT8SCR   R-squared:                       0.844
Model:                            OLS   Adj. R-squared:                  0.843
Method:                 Least Squares   F-statistic:                     868.5
Date:                Tue, 09 Dec 2025   Prob (F-statistic):               0.00
Time:                        21:03:47   Log-Likelihood:                 3411.9
No. Observations:                2902   AIC:                            -6786.
Df Residuals:                    2883   BIC:                            -6672.
Df Model:                          18                                         
Covariance Type:            nonrobust                                         
========================================================================================================
                                           coef    std err          t      P>|t|      [0.025      0.975]
--------------------------------------------------------------------------------------------------------
Intercept                                4.6270      0.016    280.473      0.000       4.595       4.659
OFSTEDRATING[T.Outstanding]              0.0552      0.004     12.597      0.000       0.047       0.064
OFSTEDRATING[T.Requires improvement]    -0.0517      0.005    -11.427      0.000      -0.061      -0.043
OFSTEDRATING[T.Serious Weaknesses]      -0.0603      0.016     -3.715      0.000      -0.092      -0.028
OFSTEDRATING[T.Special Measures]        -0.0952      0.019     -5.017      0.000      -0.132      -0.058
gor_name[T.East of England]              0.0057      0.006      0.897      0.370      -0.007       0.018
gor_name[T.London]                       0.0267      0.007      4.078      0.000       0.014       0.040
gor_name[T.North East]                   0.0203      0.008      2.405      0.016       0.004       0.037
gor_name[T.North West]                  -0.0139      0.006     -2.287      0.022      -0.026      -0.002
gor_name[T.South East]                  -0.0128      0.006     -2.119      0.034      -0.025      -0.001
gor_name[T.South West]                   0.0254      0.007      3.863      0.000       0.013       0.038
gor_name[T.West Midlands]                0.0059      0.006      0.931      0.352      -0.006       0.018
gor_name[T.Yorkshire and the Humber]     0.0200      0.007      3.046      0.002       0.007       0.033
ADMPOL_PT[T.OTHER NON SEL]               0.0154      0.006      2.529      0.011       0.003       0.027
ADMPOL_PT[T.SEL]                         0.0807      0.010      8.210      0.000       0.061       0.100
log_PTFSM6CLA1A                         -0.0699      0.004    -18.950      0.000      -0.077      -0.063
log_PERCTOT                             -0.2245      0.007    -30.152      0.000      -0.239      -0.210
log_PNUMEAL                              0.0180      0.002     11.109      0.000       0.015       0.021
PTPRIORLO                               -0.0069      0.000    -31.525      0.000      -0.007      -0.007
==============================================================================
Omnibus:                      117.971   Durbin-Watson:                   1.799
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              180.406
Skew:                          -0.370   Prob(JB):                     6.69e-40
Kurtosis:                       3.972   Cond. No.                         346.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Code

library(performance)
library(jtools)

england_filtered_clean <- england_filtered_clean %>%
  filter(PTFSM6CLA1A > 0, PERCTOT > 0, PNUMEAL > 0)

england_model3 <- lm(log(ATT8SCR) ~ log(PTFSM6CLA1A) + log(PERCTOT) + RELCHAR_Grp, data = england_filtered_clean)
summary(england_model3)


Call:
lm(formula = log(ATT8SCR) ~ log(PTFSM6CLA1A) + log(PERCTOT) + 
    RELCHAR_Grp, data = england_filtered_clean)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.37259 -0.06589 -0.00213  0.06103  0.76031 

Coefficients:
                          Estimate Std. Error t value Pr(>|t|)    
(Intercept)               5.058526   0.015456 327.295   <2e-16 ***
log(PTFSM6CLA1A)         -0.112548   0.003571 -31.516   <2e-16 ***
log(PERCTOT)             -0.400243   0.008238 -48.585   <2e-16 ***
RELCHAR_GrpChristian     -0.004545   0.005082  -0.894    0.371    
RELCHAR_GrpNon-Christian -0.013948   0.014850  -0.939    0.348    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.102 on 2956 degrees of freedom
Multiple R-squared:  0.7092,    Adjusted R-squared:  0.7088 
F-statistic:  1802 on 4 and 2956 DF,  p-value: < 2.2e-16

Code

england_model4 <- lm(log(ATT8SCR) ~ log(PTFSM6CLA1A) + log(PERCTOT) + gor_name, data = england_filtered_clean, na.action = na.exclude)
summary(england_model4)


Call:
lm(formula = log(ATT8SCR) ~ log(PTFSM6CLA1A) + log(PERCTOT) + 
    gor_name, data = england_filtered_clean, na.action = na.exclude)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.39840 -0.06023 -0.00054  0.05878  0.71757 

Coefficients:
                                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)                       5.0107282  0.0153085 327.317  < 2e-16 ***
log(PTFSM6CLA1A)                 -0.1318266  0.0037583 -35.076  < 2e-16 ***
log(PERCTOT)                     -0.3615186  0.0083599 -43.244  < 2e-16 ***
gor_nameEast Midlands            -0.0101682  0.0076764  -1.325 0.185402    
gor_nameEast of England          -0.0032498  0.0070509  -0.461 0.644903    
gor_nameLondon                    0.0885951  0.0071258  12.433  < 2e-16 ***
gor_nameNorth East                0.0716603  0.0097712   7.334 2.88e-13 ***
gor_nameNorth West               -0.0002658  0.0068006  -0.039 0.968826    
gor_nameSouth West                0.0206193  0.0073599   2.802 0.005118 ** 
gor_nameWest Midlands             0.0216499  0.0071195   3.041 0.002379 ** 
gor_nameYorkshire and the Humber  0.0272177  0.0074654   3.646 0.000271 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.09737 on 2950 degrees of freedom
Multiple R-squared:  0.7357,    Adjusted R-squared:  0.7348 
F-statistic: 821.1 on 10 and 2950 DF,  p-value: < 2.2e-16

Code

england_model5 <- lm(log(ATT8SCR) ~ log(PTFSM6CLA1A) + log(PERCTOT) + log(PNUMEAL) + gor_name, data = england_filtered_clean, na.action = na.exclude)
summary(england_model5)


Call:
lm(formula = log(ATT8SCR) ~ log(PTFSM6CLA1A) + log(PERCTOT) + 
    log(PNUMEAL) + gor_name, data = england_filtered_clean, na.action = na.exclude)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.40707 -0.05726  0.00153  0.05906  0.66397 

Coefficients:
                                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)                       4.9559677  0.0158886 311.920  < 2e-16 ***
log(PTFSM6CLA1A)                 -0.1463138  0.0039338 -37.194  < 2e-16 ***
log(PERCTOT)                     -0.3397722  0.0084583 -40.170  < 2e-16 ***
log(PNUMEAL)                      0.0206186  0.0019433  10.610  < 2e-16 ***
gor_nameEast Midlands            -0.0004914  0.0075902  -0.065 0.948380    
gor_nameEast of England           0.0007515  0.0069315   0.108 0.913676    
gor_nameLondon                    0.0745376  0.0071191  10.470  < 2e-16 ***
gor_nameNorth East                0.0963456  0.0098697   9.762  < 2e-16 ***
gor_nameNorth West                0.0098559  0.0067434   1.462 0.143966    
gor_nameSouth West                0.0343067  0.0073388   4.675 3.08e-06 ***
gor_nameWest Midlands             0.0256262  0.0069986   3.662 0.000255 ***
gor_nameYorkshire and the Humber  0.0359445  0.0073741   4.874 1.15e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.09558 on 2949 degrees of freedom
Multiple R-squared:  0.7454,    Adjusted R-squared:  0.7445 
F-statistic: 784.9 on 11 and 2949 DF,  p-value: < 2.2e-16

Code

england_model6 <- lm(log(ATT8SCR) ~ log(PTFSM6CLA1A) + log(PERCTOT) + log(PNUMEAL) + OFSTEDRATING + gor_name, data = england_filtered_clean, na.action = na.exclude)
summary(england_model6)


Call:
lm(formula = log(ATT8SCR) ~ log(PTFSM6CLA1A) + log(PERCTOT) + 
    log(PNUMEAL) + OFSTEDRATING + gor_name, data = england_filtered_clean, 
    na.action = na.exclude)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.39799 -0.05644  0.00150  0.05800  0.54719 

Coefficients:
                                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)                       4.841810   0.017103 283.105  < 2e-16 ***
log(PTFSM6CLA1A)                 -0.140453   0.003814 -36.829  < 2e-16 ***
log(PERCTOT)                     -0.293625   0.008762 -33.510  < 2e-16 ***
log(PNUMEAL)                      0.017114   0.001899   9.011  < 2e-16 ***
OFSTEDRATINGOutstanding           0.067858   0.005310  12.779  < 2e-16 ***
OFSTEDRATINGRequires improvement -0.051879   0.005492  -9.445  < 2e-16 ***
OFSTEDRATINGSerious Weaknesses   -0.039225   0.019715  -1.990   0.0467 *  
OFSTEDRATINGSpecial Measures     -0.090715   0.023054  -3.935 8.52e-05 ***
gor_nameEast Midlands             0.004759   0.007336   0.649   0.5166    
gor_nameEast of England           0.001422   0.006674   0.213   0.8313    
gor_nameLondon                    0.071049   0.006851  10.371  < 2e-16 ***
gor_nameNorth East                0.085795   0.009534   8.999  < 2e-16 ***
gor_nameNorth West                0.016287   0.006545   2.489   0.0129 *  
gor_nameSouth West                0.033397   0.007066   4.727 2.39e-06 ***
gor_nameWest Midlands             0.027829   0.006750   4.123 3.85e-05 ***
gor_nameYorkshire and the Humber  0.033224   0.007109   4.673 3.10e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.09112 on 2886 degrees of freedom
  (59 observations deleted due to missingness)
Multiple R-squared:  0.7694,    Adjusted R-squared:  0.7682 
F-statistic: 642.1 on 15 and 2886 DF,  p-value: < 2.2e-16

Code

england_model7 <- lm(log(ATT8SCR) ~ log(PTFSM6CLA1A) + log(PERCTOT) + log(PNUMEAL) + OFSTEDRATING + gor_name + PTPRIORLO + ADMPOL_PT, data = england_filtered_clean, na.action = na.exclude)
summary(england_model7)


Call:
lm(formula = log(ATT8SCR) ~ log(PTFSM6CLA1A) + log(PERCTOT) + 
    log(PNUMEAL) + OFSTEDRATING + gor_name + PTPRIORLO + ADMPOL_PT, 
    data = england_filtered_clean, na.action = na.exclude)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.37723 -0.04528  0.00333  0.04912  0.30081 

Coefficients:
                                      Estimate Std. Error t value Pr(>|t|)    
(Intercept)                          4.6296089  0.0154652 299.356  < 2e-16 ***
log(PTFSM6CLA1A)                    -0.0699264  0.0036900 -18.950  < 2e-16 ***
log(PERCTOT)                        -0.2244960  0.0074455 -30.152  < 2e-16 ***
log(PNUMEAL)                         0.0179676  0.0016174  11.109  < 2e-16 ***
OFSTEDRATINGOutstanding              0.0551690  0.0043794  12.597  < 2e-16 ***
OFSTEDRATINGRequires improvement    -0.0516629  0.0045211 -11.427  < 2e-16 ***
OFSTEDRATINGSerious Weaknesses      -0.0602663  0.0162207  -3.715 0.000207 ***
OFSTEDRATINGSpecial Measures        -0.0951661  0.0189679  -5.017 5.56e-07 ***
gor_nameEast Midlands                0.0128394  0.0060587   2.119 0.034161 *  
gor_nameEast of England              0.0185393  0.0056555   3.278 0.001058 ** 
gor_nameLondon                       0.0395373  0.0058383   6.772 1.53e-11 ***
gor_nameNorth East                   0.0331207  0.0080787   4.100 4.25e-05 ***
gor_nameNorth West                  -0.0010765  0.0054833  -0.196 0.844374    
gor_nameSouth West                   0.0382890  0.0059572   6.427 1.51e-10 ***
gor_nameWest Midlands                0.0187024  0.0057100   3.275 0.001068 ** 
gor_nameYorkshire and the Humber     0.0328390  0.0060105   5.464 5.06e-08 ***
PTPRIORLO                           -0.0069371  0.0002201 -31.525  < 2e-16 ***
ADMPOL_PTNON SEL IN HIGHLY SEL AREA -0.0154098  0.0060930  -2.529 0.011488 *  
ADMPOL_PTSEL                         0.0652773  0.0077220   8.453  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.07492 on 2883 degrees of freedom
  (59 observations deleted due to missingness)
Multiple R-squared:  0.8443,    Adjusted R-squared:  0.8433 
F-statistic: 868.5 on 18 and 2883 DF,  p-value: < 2.2e-16

Code

#Get fitted values with NA for excluded rows
fitted_vals <- fitted(england_model7)

# Add fitted values to the dataframe
england_filtered_clean$fitted7 <- fitted_vals

Task 4 - Evaluation

When you have your ‘best’ model, how do you interpret the coefficients?
- Which variable(s) has(have) the most explanatory power (check t-values for this)?
- How do you interpret the combined explanatory power of variables in your model?
- What kind of confounding do you observe as you add more variables (if any)?
- Do you have any issues of multicollinearity or residual independence? Does your model pass the standard tests?
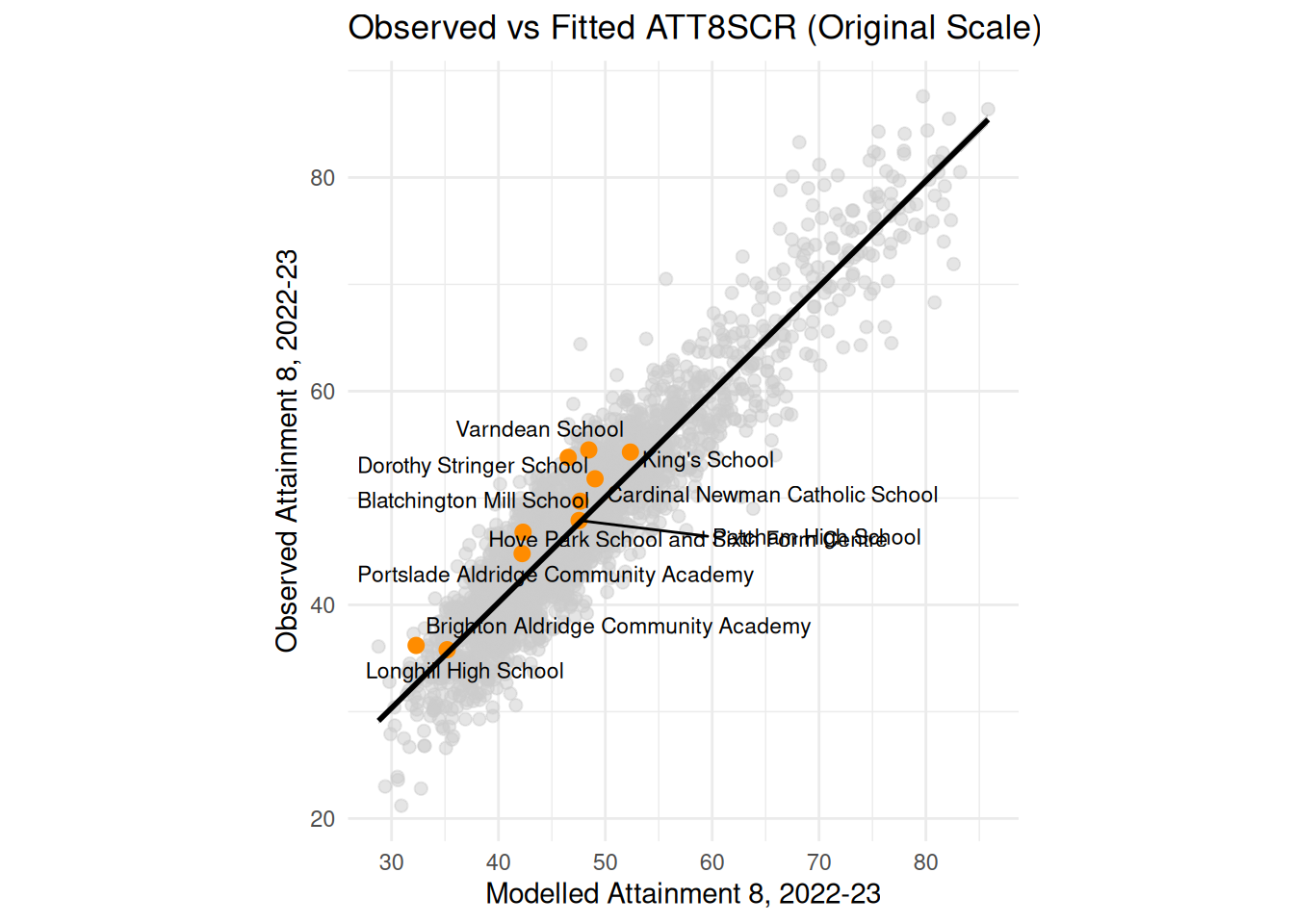
- You should also plot your model estimates (fitted values) against your original \(Y\) variable as I have done below (possibly overlay your local authorities from last week as well) and map your residuals too.

Here’s my best model in R compared with some of the others I built as I went along:

Code

names(coef(england_model3))

[1] "(Intercept)"              "log(PTFSM6CLA1A)"        
[3] "log(PERCTOT)"             "RELCHAR_GrpChristian"    
[5] "RELCHAR_GrpNon-Christian"

Code

coef_names <- c(
  "Constant" = "(Intercept)",
  #"Religious Christian" = "RELCHAR_GrpChristian",
  #"Religious not-Christian","RELCHAR_GrpNon-Christian",
  "% Disadvantaged end KS4 (log)" = "log(PTFSM6CLA1A)",
  "% overall absence (log)" = "log(PERCTOT)",
  "% English Not First Language (log)" = "log(PNUMEAL)",
  "Ofsted: Outstanding" = "OFSTEDRATINGOutstanding",
  "Ofsted: Requires Improvement" = "OFSTEDRATINGRequires improvement",
  "Ofsted: Serious Weaknesses" = "OFSTEDRATINGSerious Weaknesses",
  "Ofsted: Special Measures" = "OFSTEDRATINGSpecial Measures",
  "Region: East Midlands" = "gor_nameEast Midlands",
  "Region: East of England" = "gor_nameEast of England",
  "Region: London" = "gor_nameLondon",
  "Region: North East" = "gor_nameNorth East",
  "Region: North West" = "gor_nameNorth West",
  "Region: South West" = "gor_nameSouth West",
  "Region: West Midlands" = "gor_nameWest Midlands",
  "Region: Yorkshire and the Humber" = "gor_nameYorkshire and the Humber",
  "% Low Prior Attainment" = "PTPRIORLO",
  "Admissions: Non-selective in Highly Selective Area" = "ADMPOL_PTNON SEL IN HIGHLY SEL AREA",
  "Admissions: Selective" = "ADMPOL_PTSEL"
)

Code

library(jtools)

export_summs(
  england_model3, england_model4, england_model5, england_model6, england_model7, 
  robust = "HC3",
  coefs = coef_names
)

	Model 1	Model 2	Model 3	Model 4	Model 5
Constant	5.06 ***	5.01 ***	4.96 ***	4.84 ***	4.63 ***
	(0.02)	(0.02)	(0.02)	(0.02)	(0.02)
% Disadvantaged end KS4 (log)	-0.11 ***	-0.13 ***	-0.15 ***	-0.14 ***	-0.07 ***
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)
% overall absence (log)	-0.40 ***	-0.36 ***	-0.34 ***	-0.29 ***	-0.22 ***
	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)
% English Not First Language (log)			0.02 ***	0.02 ***	0.02 ***
			(0.00)	(0.00)	(0.00)
Ofsted: Outstanding				0.07 ***	0.06 ***
				(0.01)	(0.00)
Ofsted: Requires Improvement				-0.05 ***	-0.05 ***
				(0.01)	(0.01)
Ofsted: Serious Weaknesses				-0.04	-0.06 **
				(0.02)	(0.02)
Ofsted: Special Measures				-0.09 ***	-0.10 ***
				(0.02)	(0.02)
Region: East Midlands		-0.01	-0.00	0.00	0.01 *
		(0.01)	(0.01)	(0.01)	(0.01)
Region: East of England		-0.00	0.00	0.00	0.02 ***
		(0.01)	(0.01)	(0.01)	(0.01)
Region: London		0.09 ***	0.07 ***	0.07 ***	0.04 ***
		(0.01)	(0.01)	(0.01)	(0.01)
Region: North East		0.07 ***	0.10 ***	0.09 ***	0.03 ***
		(0.01)	(0.01)	(0.01)	(0.01)
Region: North West		-0.00	0.01	0.02 *	-0.00
		(0.01)	(0.01)	(0.01)	(0.01)
Region: South West		0.02 **	0.03 ***	0.03 ***	0.04 ***
		(0.01)	(0.01)	(0.01)	(0.01)
Region: West Midlands		0.02 **	0.03 ***	0.03 ***	0.02 **
		(0.01)	(0.01)	(0.01)	(0.01)
Region: Yorkshire and the Humber		0.03 ***	0.04 ***	0.03 ***	0.03 ***
		(0.01)	(0.01)	(0.01)	(0.01)
% Low Prior Attainment					-0.01 ***
					(0.00)
Admissions: Non-selective in Highly Selective Area					-0.02 *
					(0.01)
Admissions: Selective					0.07 ***
					(0.01)
N	2961	2961	2961	2902	2902
R2	0.71	0.74	0.75	0.77	0.84
Standard errors are heteroskedasticity robust. * p < 0.001; p < 0.01; * p < 0.05.

Code

check_model(england_model7)

Code

library(tidyverse)
library(ggrepel)

# Convert fitted values back to original scale
england_filtered_clean <- england_filtered_clean %>%
  mutate(
    fitted_original = exp(fitted7),
    highlight = LANAME == "Brighton and Hove",
    label = if_else(highlight, SCHNAME.x, NA_character_)
  )

# Scatter plot with layered points and full-model fit line
ggplot(england_filtered_clean, aes(x = fitted_original, y = ATT8SCR)) +
  # All schools in grey
  geom_point(color = "grey80", alpha = 0.5, size = 2) +

  # Brighton and Hove schools in orange
  geom_point(data = filter(england_filtered_clean, highlight),
             aes(x = fitted_original, y = ATT8SCR),
             color = "darkorange", size = 2.5) +

  # Labels for Brighton and Hove schools
  geom_text_repel(data = filter(england_filtered_clean, highlight),
                  aes(label = label),
                  size = 3, max.overlaps = 20) +

  # Line of best fit for all schools
  geom_smooth(method = "lm", se = TRUE, color = "black") +
  
# Mirror x and y axes
  coord_equal() +


  theme_minimal() +
  labs(
    title = "Observed vs Fitted ATT8SCR (Original Scale)",
    x = "Modelled Attainment 8, 2022-23",
    y = "Observed Attainment 8, 2022-23"
  )

Code

# Filter for Brighton and Hove only
brighton_data <- england_filtered_clean %>%
  filter(LANAME == "Brighton and Hove")

# Plot with regression line
ggplot(brighton_data, aes(x = fitted_original, y = ATT8SCR)) +
  geom_point(color = "darkorange", size = 2) +
  geom_smooth(method = "lm", se = TRUE, color = "black") +
  geom_text_repel(aes(label = SCHNAME.x), max.overlaps = 20, size = 3) +
  theme_minimal() +
  labs(
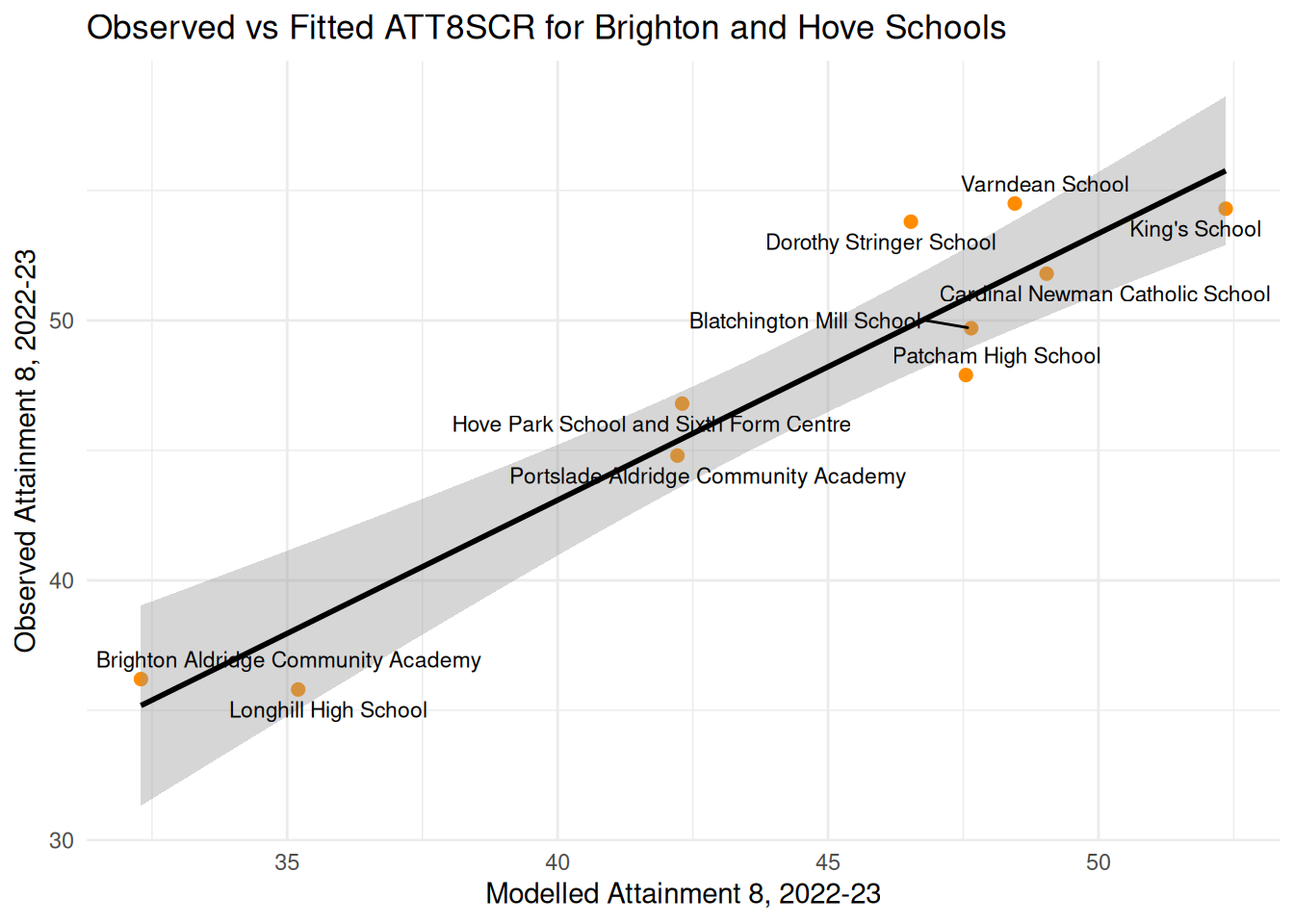
    title = "Observed vs Fitted ATT8SCR for Brighton and Hove Schools",
    x = "Modelled Attainment 8, 2022-23",
    y = "Observed Attainment 8, 2022-23"
  )

Code

library(tidyverse)

# Calculate residuals and filter for Brighton and Hove
brighton_residuals <- england_filtered_clean %>%
  filter(LANAME == "Brighton and Hove") %>%
  mutate(
    fitted_original = exp(fitted7),
    residual = ATT8SCR - fitted_original,
    abs_residual = abs(residual)
  )

# Create a bar plot centered on zero
ggplot(brighton_residuals, aes(x = reorder(SCHNAME.x, residual), y = residual)) +
  geom_col(fill = "darkorange") +
  geom_hline(yintercept = 0, linetype = "dashed", color = "grey40") +
  coord_flip() +
  theme_minimal() +
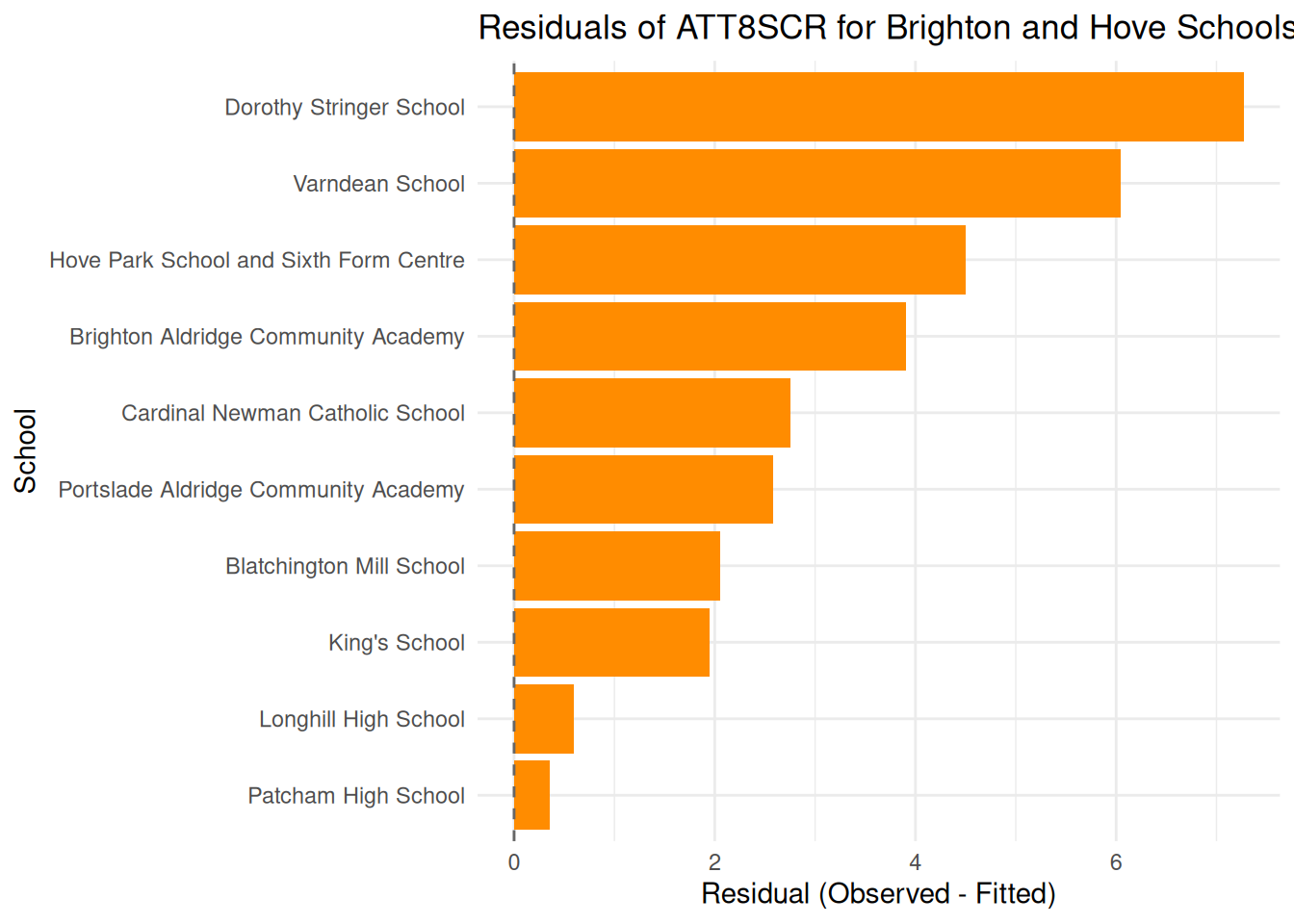
  labs(
    title = "Residuals of ATT8SCR for Brighton and Hove Schools",
    x = "School",
    y = "Residual (Observed - Fitted)"
  )

Task 5 - Interacting Variables (Extension activity)

In the lecture, you saw how we could look at how some of the continuous variables (like disadvantage or absence) vary by categorical variable levels (like region). Or indeed, whether continuous variables might interact with each other - for example do levels of unauthorised absence and disadvantage affect each other.

As you saw in the lecture, interpreting interactions can be complex, so here I would just like you to have a brief experiment with some of the variables in your best model.

If you are struggling to understand these effects, again, an AI helper like Gemini or ChatGPT might help you understand these interactions if you feed it your model outputs.

Most of the time in most of the regression models you build, you might not need to interact variables, but it can be informative. Next week, however, we will look at other alternatives to interacting variables when we move onto linear mixed effects models. So at this point, just some experimentation is what I would like you to achieve.