Measuring Relationship

Huanfa Chen - huanfa.chen@ucl.ac.uk

25th October 2025

Last week

Lecture 4 - linear algebra

Looked at:

Can use mathematical notation to write equations in a univeral language
Linear algebra helps us to solve systems of linear equations

This week

Objectives

Understand and calculate Pearson and Spearman correlation between two variables.
Understand the difference between Pearson and Spearman correlation.
Understand ANOVA.

Classification of statistical analysis

Univariate analysis (for one variable) (W1/2)
Bivariate analysis (for two variables) (W5)
Multivariate analysis (for multiple variables) (Further weeks; very common in GIS)

Back to W1: Descriptive statistics of each variable

The most basic statistical information about the dataset and each variable (separately)

Sample size
Mean, median, mode
Variance, standard deviation
Range

Variance: quantifying spread

Denote city population by \([y_1, y_2, ..., y_n]\) and variance by \(\sigma^2\)

\[ \begin{aligned} \sigma^2 &= \frac{\sum_{i=1}^{n} (y_i - \bar{y})^2}{n} \\ &= \frac{(y_1 - \bar{y})^2 + (y_2 - \bar{y})^2 + \dots + (y_n - \bar{y})^2}{n} \end{aligned} \]

Checklist when you learn a new metric …

Let’s take variance as an exmaple

Questions	Answer
Does it exist for all inputs?	Yes
Meaning of sign (+/-)	Non-negative; 0 means all values are identical
Range	[0, \(\infty\))
Is it normalised (i.e. in [-1,1] or [0,1])	No
Is it symmetric, if it involves multiple inputs?	N/A

Extending variance to two variables: do A and B change in the same direction? To what extent?

Examples:

Is the transport accessibility of a neighbourhood related to average housing price?
Is a student’s attendance in Quantitative Methods related to their performance in the module?
For schools in England, is the proportion of pupils who are disadvantaged related to the average attainment 8 score? [social & education inequality]

Covariance

\[ \mathrm{Cov}(x, y) = \frac{1}{n} \sum_{i=1}^{n} \left( x_i - \bar{x} \right) \left( y_i - \bar{y} \right) \]

Example

Compute row by row before summing up

	x - x̄	y - ȳ	(x - x̄)(y - ȳ)
1	-2.25	-1.78	3.99
2	2.15	-2.08	-4.46
3	-1.55	2.32	-3.6
4	1.65	1.52	2.52

Covariance = (3.99 + -4.46 + -3.60 + 2.52) / 4 = -0.39

Checklist for covariance

Questions	Answer
Does it exist for all inputs?	Yes
Meaning of sign (+/-)	Positive: x, y change in the same direction
Range	(-\(\infty\), \(\infty\))
Is it normalised (i.e. in [-1,1] or [0,1])	No
Is it symmetric, if it involves multiple inputs?	Yes, cov(x,y)=cov(y,x)

Crisis of covariance: incomparable

Does Cov = -0.39 tell how much x and y change together, apart from the direction?
Assuem three variables A,B,C.
- Cov(A,B) = -0.39
- Cov(A,C) = -0.01
- Can we say which A and B are more closely related compared with A and C?
- No

Improvements

Factors underlying Cov(A,B)
1. Direction & extent of A and B changing together
2. Magnitude of variability in A and B separately
Ideally, we want to remove #2.
Normalisation is the solution. But how?

Pearson correlation

Definition

\[ r_{xy} = \frac{\mathrm{Cov}(X, Y)}{\sigma_X \, \sigma_Y} = \frac{\frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})} {\sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2} \; \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \bar{y})^2}} \]

\(\sigma_X\) denotes the standard deviation of \(x\) variable.
Used to measure the linear relationship between two variables.
How close the data points fall on a straight line

Quiz: what is the unit of Covariance and Correlation?

unit of values is very important in quantitative analysis. \[ \mathrm{Cov}(x, y) = \frac{1}{n} \sum_{i=1}^{n} \left( x_i - \bar{x} \right) \left( y_i - \bar{y} \right) \]
You are investigating the relationship between outdoor temperature (in unit of \(^\circ\text{C}\)) and fire service call rates (in unit of \(\text{minute}^{-1}\)). What is the unit of the covariance?
A. \(^\circ\text{C} \cdot \text{minute}^{-1}\)
B. unitless
C. \(^\circ\text{C}\)
D. \(^{\circ}\text{C}^{2} \cdot \text{minute}^{-2}\)

In the same analysis, what is the unit of correlation?

A. \(^\circ\text{C} \cdot \text{minute}^{-1}\)
B. unitless
C. \(^\circ\text{C}\)
D. \(^{\circ}\text{C}^{2} \cdot \text{minute}^{-2}\)

History of Pearson correlation

Francis Galton
Image credit: https://commons.wikimedia.org/wiki/File:Portrait_of_Francis_Galton._Wellcome_M0002305.jpg

Karl Pearson
Image credit: https://commons.wikimedia.org/wiki/File:Karl_Pearson,_1912.jpg

This idea was developed by Karl Pearson, based on earlier idea from Francis Galton (in 1880s).
Karl Pearson is also known for other significant contributions to statistics, including chi-square test.
\(\chi^2 = \sum_{i=1}^{k} \frac{(O_i - E_i)^2}{E_i}\), measures how closely the observed data match the expected values.

Checklist of Pearson correlation

Questions	Answer
Does it exist for all inputs?	Not when variance of x or y equals 0
Meaning of sign (+/-)	Positive: x, y change in the same direction
Range	[-1, 1]
Is it normalised (i.e. in [-1,1] or [0,1])	Yes
Is it symmetric, if it involves multiple inputs?	Yes, Cor(x,y)=Cor(y,x)

Hypothesis testing and p-values of Pearson correlation

import numpy as np
from scipy import stats
res = stats.spearmanr([1, 2, 3, 4, 5], [5, 6, 7, 8, 7])
print(f"Pearson correlation = {res.statistic:.4f}")
print(f"P value = {res.pvalue:.4f}")

Pearson correlation = 0.8208
P value = 0.0886

Back to hypothesis testing

There are various ways to test if Pearson correlation is statistically significant.
One way is using Student’s t-distribution, assuming X & Y have a bivariate normal distribution.
\(H_0\) (null hypothesis): no correlation between X & Y (or cor = 0) \[ t = \frac{r}{\sigma_r} = \frac{r \sqrt{n - 2}}{\sqrt{1 - r^2}} \]

Where:
- \(t\) = t-statistic
- \(r\) = calculated Pearson correlation coefficient
- \(n\) = number of paired observations

Examples

Question: does cor = 0 mean no relationship between X and Y? NO

Image credit: https://commons.wikimedia.org/wiki/File:Correlation_examples.png

#1 Limitation: not working well with non-linear relationship

Pearson correlation only measures linear association between X and Y.
It is not a good metric of association if the scatterplot has a non-linear or curved pattern.
When presenting the correlation, it is always good to include a scatterplot.

#2 Limitation: sensitivity to ourliers

Pearson correlation involves the average of X and Y and difference between values.
Therefore, it is sensitive to outliers.
Again, a scatterplot will help detect outliers.
If there are obvious ouliers in the data, please address them before conducting analysis.

#3 Limitations: not working with nominal or ordinal data

Pearson correlation doesn’t work for nominal or ordinal data
… as we can’t compute the mean or difference of nominal/ordinal data.

Spearman correlation (Spearman’s Rho)

Motivation

If I’d like to check if X and Y are consistenly increasing/decreasing (aka monotonic), rather than if they fall on a line
How can I achieve it?
monotonic relationship is a more general than linear relationship.
For example, \(y = x^3\) is monotonic but not linear.
Solution: rank X and Y separately, and then calculate Pearson correlation on the ranked values (rather than orignal values).

Example

Original Values:

	0	1	2	3	4	5	6	7	8	9
x	0.55	0.72	0.6	0.54	0.42	0.65	0.44	0.89	0.96	0.38
y	0.79	0.53	0.57	0.93	0.07	0.09	0.02	0.83	0.78	0.87

Step 1: Ranks:

	0	1	2	3	4	5	6	7	8	9
rank_x	5	8	6	4	2	7	3	9	10	1
rank_y	7	4	5	10	2	3	1	8	6	9

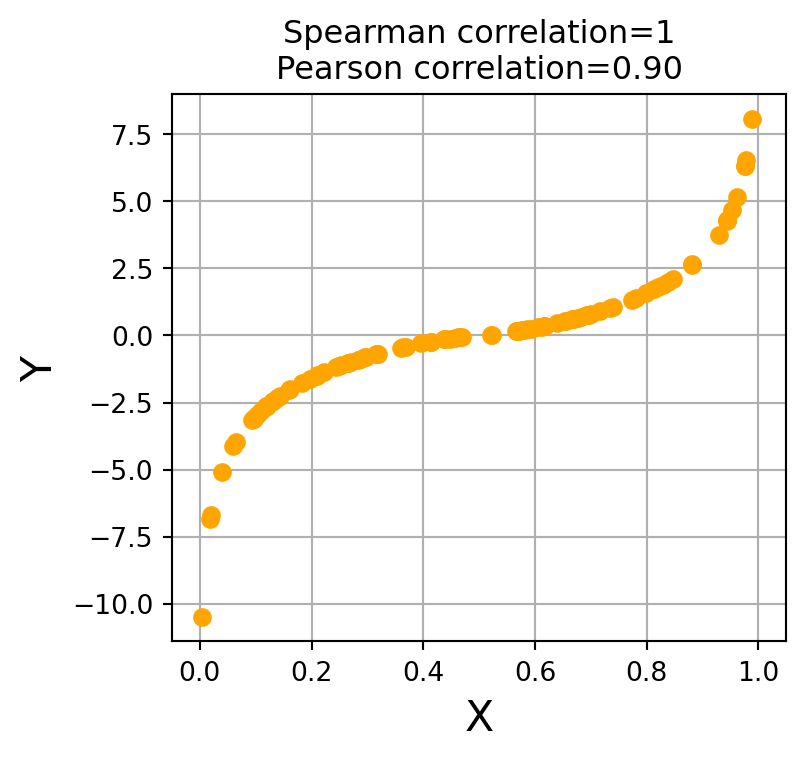
Step 2: Spearman Correlation = 0.0424

Examples

Spearman correlation doesn’t tell if or how much the relationship is linear
Spearman & Pearson correlation on the same data are incomparable, as they tell different things.

<Figure size 960x480 with 0 Axes>

Spearman correlation is robust to ourliers (more than Pearson correlation)

On original data, increase the largest X value by 1000

Original Pearson C = 0.3350, Spearman C = 0.0424

Updated Values

0	1	2	3	4	5	6	7	8	9
0.55	0.72	0.6	0.54	0.42	0.65	0.44	0.89	1000.96	0.38
0.79	0.53	0.57	0.93	0.07	0.09	0.02	0.83	0.78	0.87

Updated Pearson C = 0.2261, Spearman C = 0.0424

Spearman correlation applies to ordinal data (while Pearson correlation doesn’t)

	Nominal	Ordinal	Interval	Ratio
Pearson correlation	❌	❌	✅	✅
Spearman correlation	❌	✅	✅	✅

Potential limitation of Spearman correlation

It lies in computational cost for big data
Spearman correlation requires sorting on X and Y, which is not very efficient on big data

ANOVA (Analysis of Variance)

Motivation

Pearson/Spearman correlation applies for ordinal/interval/ratio variables.
What if we want to understand the relationship between a nominal variable and a continuous one?
For example - in school data, we have average attainment of boys and girls per school. are gender and attainment correlated?
Let’s rephrase this question as: is there a significant difference in attainment between boys and girls? (Does this sound familiar)

Back to W3 Hypothesis Testing

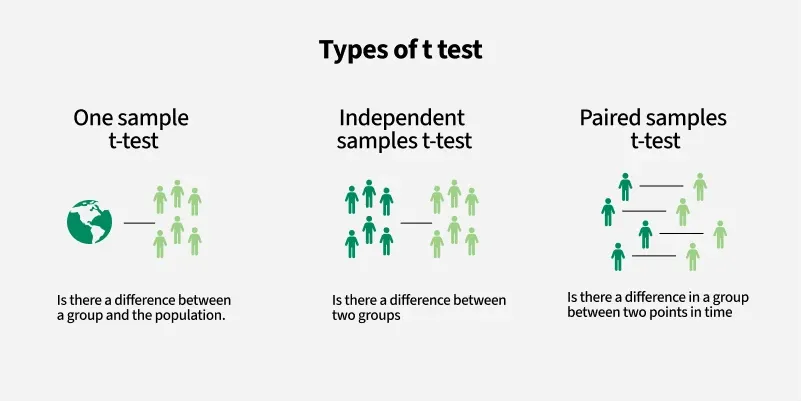
Image credit: https://www.geeksforgeeks.org/data-science/t-test/

Are gender and attainment correlated?

We can use Independent samples t-test for this task, when average attainments of boys and girls are not paired. For example, we’ve average attainments of boys from 10 schools and of girls from 8 schools.
Alternatvely, We can use Paired samples t-test, if the average attainments of boys and girls are paired by schools (i.e. data from the same schools for both groups).

Motivated continued - what if there are three or more groups?

Is there significant difference in school-average attainment across London councils of Camden, Westminster, and Islington?
ANOVA (ANalysis Of Variance): used to determine if multiple groups are statistically significantly different.

Theory behind ANOVA

Step 1: break down total variance of values into two parts. Total-variance = between-group-variance + within-group-variance
Step 2：\(F = \frac{\text{between-group variance}}{\text{within-group variance}}\)
Step 3: calculate the probability of \(F\) greater than or equal to computed \(F\). Under Null Hypothesis (there is no significant difference between groups), \(F\) follows a F-distribution and \(E[F]=1\).

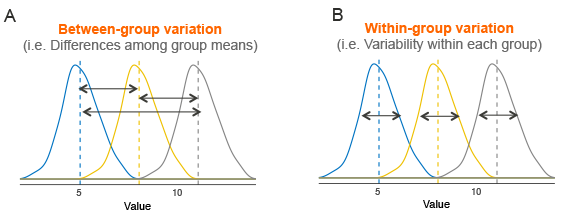
Image credit: datanovia.com

ANOVA has (many) assumptions

Independence of observations: each subject belongs to only 1 group; every observation is independent of others
No significant outliers exist
Normality: The data are approximately normally distributed
Homogeneity of variances: variance of the outcome variable should be similar in all groups
These assumptions need to be tested before conducting ANOVA

Assumptions and Testing

Assumption	Testing
Independence of observations	Design-based check, randomization review
No significant outliers	Boxplots/Z-scores; be cautious when removing outliers
Normality	Shapiro–Wilk test; Q–Q plots
Homogeneity of variances	Levene test, Welch test

ANOVA is flexible

Feature	One-Way ANOVA	Two-Way ANOVA
Purpose	Compare means of three or more groups based on one factor	Compare means based on two factors and their interaction
Example	Do school attainments vary across LA (Camden/Islington/Westminster)?	Do school attainments vary across LA (Camden/Islington/Westminster) & gender (male/female)?
Assumptions	Normality, no outliers, homogeneity of variances, independence	Same as one-way plus assumptions for interaction effects
Output	F-statistic, p-value for group differences	F-statistics and p-values for each factor and interaction effects

Key takeaways

Can use Pearson/Spearman correlation to measure the relationship between two variables.
Choose Pearson or Spearman correlation metric based on the dataset and interpret them correctly.
To measure difference between two groups, use (paired) samples t-test
To measure difference between multiple groups, use one-way ANOVA
To measure difference across two factors, use two-way ANOVA

Practical

The practical will focus on calculating and interpreting correlation metrics.
Have you questions prepared!