Clustering analysis

Huanfa Chen - huanfa.chen@ucl.ac.uk

29th November 2025

CASA0007 Quantitative Methods

Last week

Lecture 9 - dimensionality reduction

Looked at:

• Understand the motivation of dimensionality reduction
• Understand the principle of Principal Component Analysis
• Can apply PCA to school datasets or other datasets
  

This week

Objectives

• Understand the motivation and principle of clustering analysis.
• Understand K-Means and hierarchical clustering.
• Interpret the results of clustering analysis.

What is clustering

• Type of analysis that divides data points into groups based on some similarity criteria
• A cluster is a group of similar data points

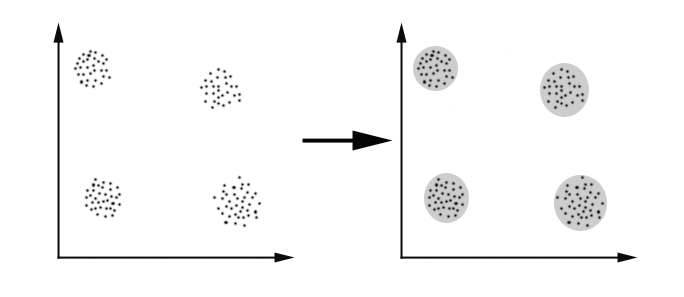
Image credit: 

Motivation of clustering

• Discover groups of similar data points
• Assist visualisation

Examples of clustering - Booth map

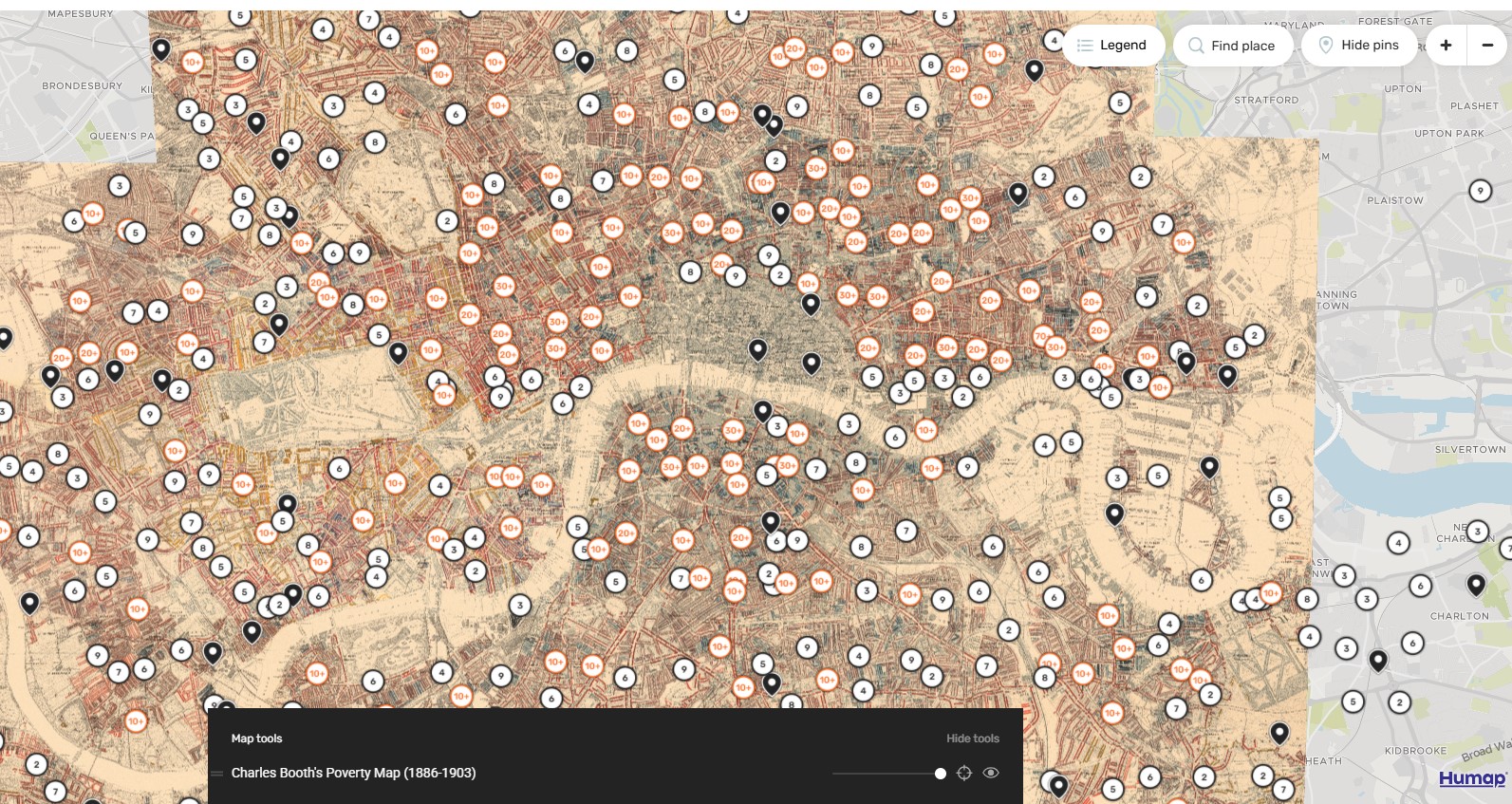
Image credit: https://booth.lse.ac.uk/map

Examples of clustering - London Output Area Classification

• Clustering OAs on 70+ socio-economic variables (non-spatial); 32000 OAs clustered into 8 groups
• Clusters have obvious spatial patterns but aren’t spatially connected

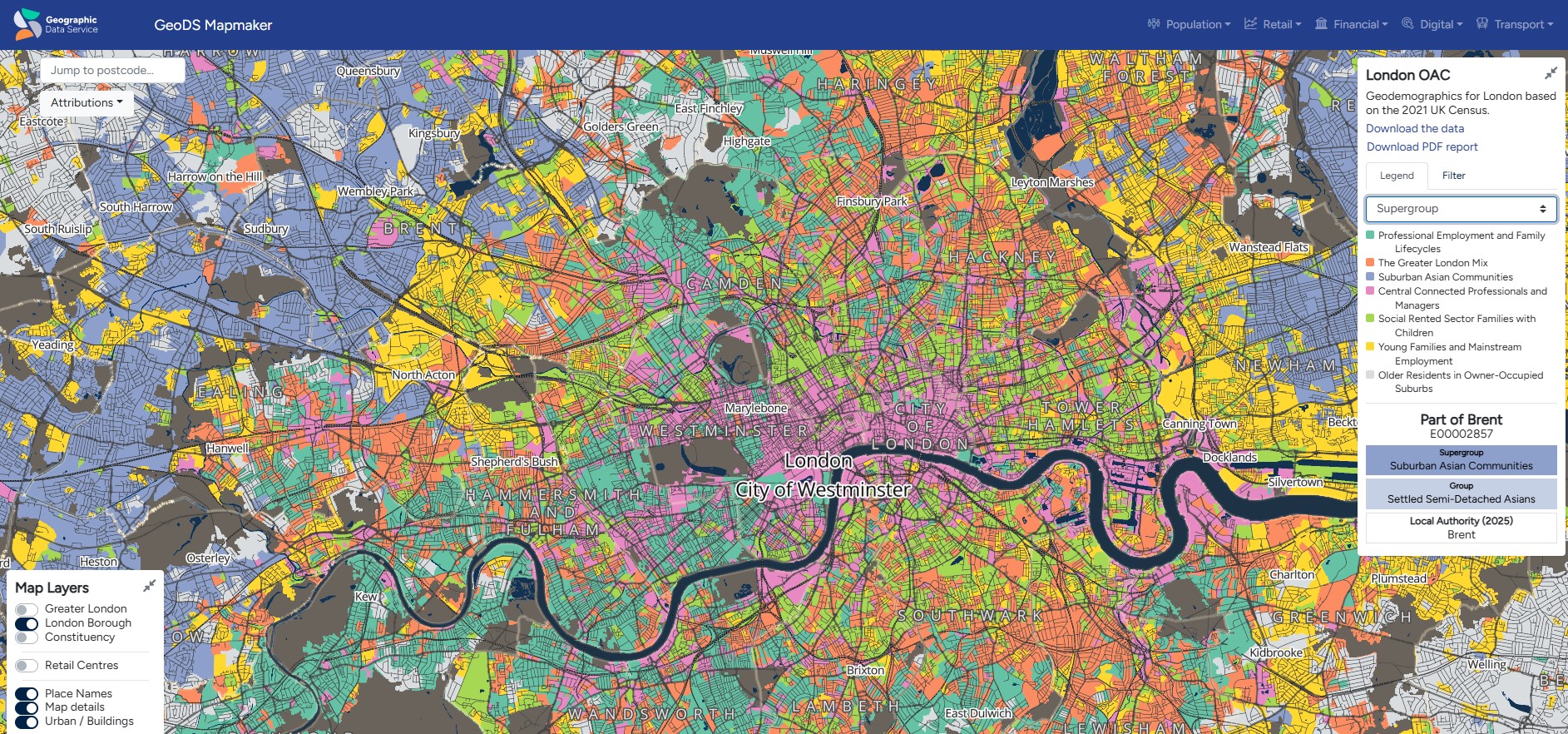
Image credit: https://mapmaker.geods.ac.uk/

Process of conducting clustering analysis

• Standardise variables
• Choose clustering algorithms (one or several)
• Select parameters of the clustering algorithm
• Interpret the results
• Finalise the clustering model

K-Means

Steps

Iterative process (Expectation-Maximisation algorithm)

• Place k centroids randomly within space
• Assign data points to nearest centroid
• Recalculate centroids as the new mean of the cluster
• Continue until centroid assignments no longer change

Implications of centroid as mean of data points in a cluster

• K-Means is incapable of handling categorical variables, as we can’t calculate the mean of a categorical variable
• K-Means is sensitive to outliers, as an outlier significantly impacts the mean of a dataset

Problems with K-Means and solutions

• Sensitive to outliers (solution: use another clustering method, or remove outliers)
• Incapable of handling categorical variables (solution: k-modes or k-prototypes)
• Requires knowledge of the number of clusters (k), which we may not know in advance (solution: Elbow method to find k)
• Sensitive to centroid initialisation, which can lead to poor solutions (solution: try multiple random initialisation and pick up the best one; initialise centroid based on data distribution)

K-Means implementation in sklearn

• class sklearn.cluster.KMeans(n_clusters=8, *, init=‘k-means++’, n_init=‘auto’, max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True, algorithm=‘lloyd’)
• By default, this function uses init=‘kmeans++’, which selects initial cluster centroids using sampling based on an empirical probability distribution of the points’ contribution to the overall inertia

K-Means implementation in sklearn: output

• cluster_centers_: ndarray of shape (n_clusters, n_features). Coordinates of cluster centers.
• labels_: ndarray of shape (n_samples,). Labels of each point
• inertia_: float. Sum of squared distances of samples to their closest cluster center, weighted by the sample weights if provided.
• n_iter_: int. Number of iterations run.
• n_features_in_: int. Number of features seen during fit.

Selecting K

1. Try different values of k.
   
2. Plot the inertia (within-cluster sum of squares).
   
3. Use the elbow method to pick a reasonable k where the decrease of inertia starts to flatten out.

Selecting K - example

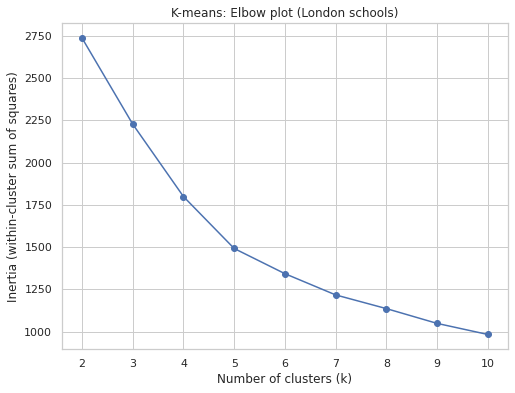
Result: k=5 is appropriate.

Hierarchical clustering

Definition

• Two ways of hierarchical clustering
  • agglomerative: bottom-up; begin with one cluster per data point and gradually merge into larger clusters.
  • divisive: top-down; begin with one big cluster and gradually split into smaller clusters

Process

• Start with every point in its own cluster
• Merge points according to a linkage criterion (or distance)
• Compute centroid of new clusters
• Expand linkage threshold and continue until all points in one cluster

Advantage of hierarchical clustering

• No prior knowledge of data required
• Users can choose the level in a hierarchy structure or use Elbow methosd (similar to K-Means)

Linkage criterion (distance between two clusters)

• ward: to minimizes the variance of the clusters being merged (default setting for sklearn AgglomerativeClustering)
• average: the average of the distances of each data points of the two clusters
• complete (or maximum): the maximum distances between all data points of the two clusters
• single: the minimum of the distances between all observations of the two sets

Example of hierarchical clustering

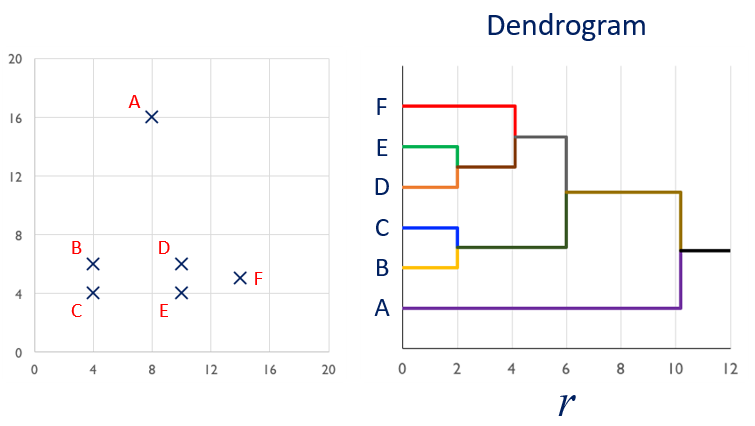
Example of hierarchical clustering (continued)

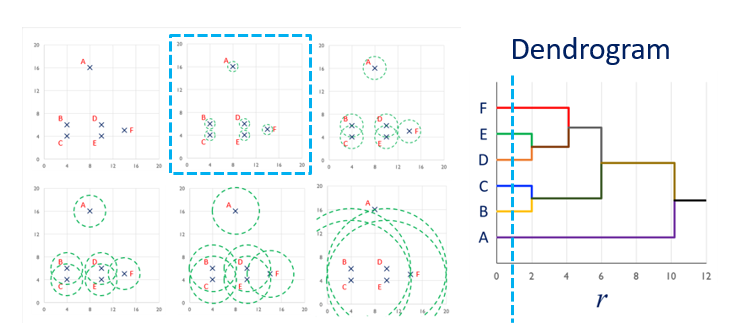
Example of hierarchical clustering (continued)

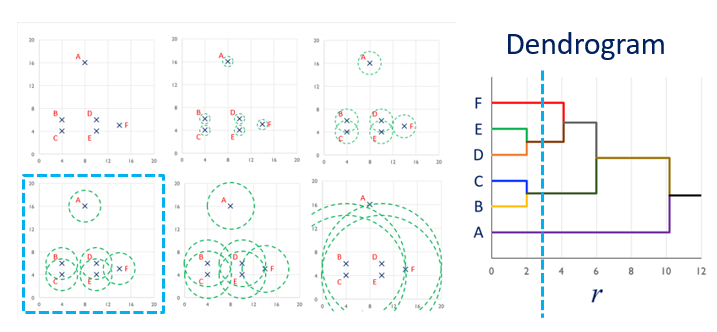
Interpreting clustering (clustering method-agnostic)

Cluster centroid as representative

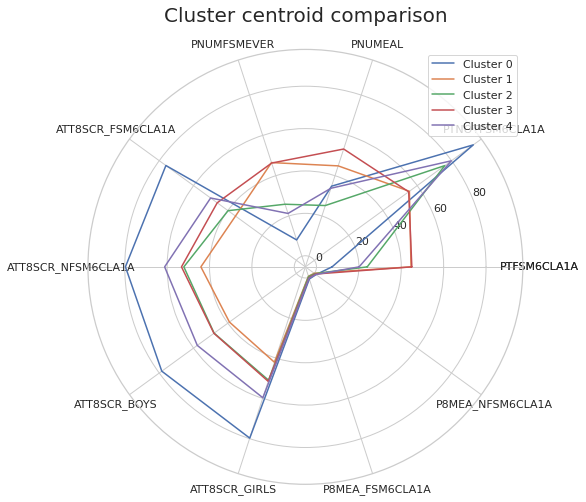
Mapping

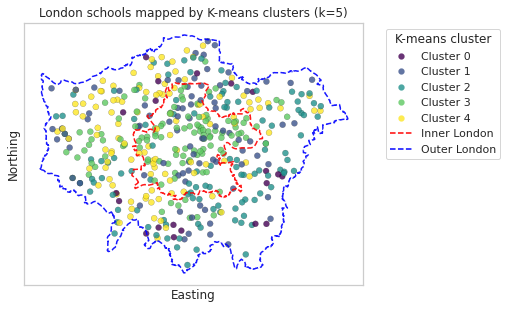
To check if schools belonging to a cluster are geographically clustered

Key takeaways

• Clustering analysis aims to identify groups within data points. It is a type of unsupervised learning.
• K-Means and hierarchical clustering are two popular clustering techniques.
• We can interpret clustering results via visualising the cluster centroids or mapping the clusters.

Practical

• The practical will focus on clustering analysis of the school data.
• Have you questions prepared!